Example of multiple overlaid probability plots
main topic     interpreting results     session command     see also 

You want to assess the efficacy of two coatings designed to reduce the flammability of fabrics. You randomly select 15 samples each of fabric with no coating, Coating A applied, and Coating B applied. Testers then hold each sample over an open flame for a fixed amount of time and measure the length of the burned portion.

You typically use the 87th percentile as a benchmark for such tests. Create probability plots for each treatment to determine if the data are fit well by normal distributions and to estimate the 87th percentile for each population.

1    Open the worksheet FLAMERTD.MTW.

2    Choose Graph > Probability Plot.

3    Choose Multiple, then click OK.

4    In Graph variables, enter Fabric - CoatingB.

5    Click Scale, then click the Percentile Lines tab.

6    In Show percentile lines at Y values, type 87.

7    Click the Gridlines tab, then uncheck all boxes. Click OK.

8    Click Distribution, then click the Data Display tab.

9    Uncheck Show confidence interval. Click OK in each dialog box.

Graph window output

Interpreting the results

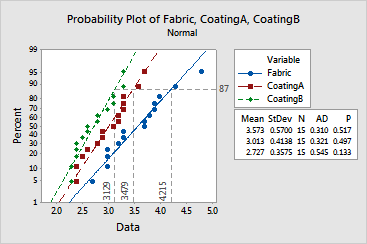
The plotted points follow the fitted distribution lines fairly closely, and the p-values for each Anderson-Darling test are greater than 0.10, suggesting that normal distributions fit these data fairly well. The estimated 87th percentiles for each population are:

·    4.215 for the uncoated fabric

·    3.479 for the fabric with Coating A

·    3.129 for the fabric with Coating B

The order of variables in the output table is the same as that in the legend.

Coating A appears to reduce fabric burn, as evidenced by the leftward shift in the fitted line and the shorter mean burn length (3.013 as compared with 3.573 for the fabric with no coating). Coating A also appears to reduce the variability in the burn lengths, as evidenced by the steeper slope of the fitted line and the smaller standard deviation (0.4138 compared to 0.5700). However, appropriate tests would need to be conducted to confirm these observations.

Coating B may be more effective than Coating A. Coating B reduced the mean burn length to 2.727 and the standard deviation to 0.3575.