Example of Accelerated Life Testing
main topic     interpreting results     session command     see also 

Suppose you want to investigate the deterioration of an insulation used for electric motors. The motors normally run between 80 and 100° C. To save time and money, you decide to use accelerated life testing.

First you gather failure times for the insulation at abnormally high temperatures - 110, 130, 150, and 170° C - to speed up the deterioration. With failure time information at these temperatures, you can then extrapolate to 80 and 100° C. It is known that an Arrhenius relationship exists between temperature and failure time.

To see how well the model fits, you will draw a probability plot based on the standardized residuals.

1    Open the worksheet INSULATE.MTW.

2    Choose Stat > Reliability/Survival > Accelerated Life Testing.

3    In Variables/Start variables, enter FailureT. In Accelerating variable, enter Temp.

4    From Relationship, choose Arrhenius.

5    Click Censor. In Use censoring columns, enter Censor, then click OK.

6    Click Graphs. In Design value to include on plot, enter 80. Click OK.

7    Click Estimate. In Enter new predictor values, enter Design, then click OK in each dialog box.

Session window output

Accelerated Life Testing: FailureT versus Temp

 

 

Response Variable: FailureT

 

Censoring Information  Count

Uncensored value          66

Right censored value      14

 

Censoring value: Censor = C

 

Estimation Method: Maximum Likelihood

 

Distribution:   Weibull

 

Relationship with accelerating variable(s):   Arrhenius

 

 

Regression Table

 

                      Standard                   95.0% Normal CI

Predictor      Coef      Error       Z      P     Lower     Upper

Intercept  -15.1874   0.986180  -15.40  0.000  -17.1203  -13.2546

Temp       0.830722  0.0350418   23.71  0.000  0.762042  0.899403

Shape       2.82462   0.256969                  2.36332   3.37596

 

Log-Likelihood = -564.693

 

 

Table of Percentiles

 

                           Standard   95.0% Normal CI

Percent  Temp  Percentile     Error    Lower    Upper

     50    80      159584   27446.9   113918   223557

     50   100     36948.6   4216.51  29543.4  46209.9

Graph window output:

 

Interpreting the results

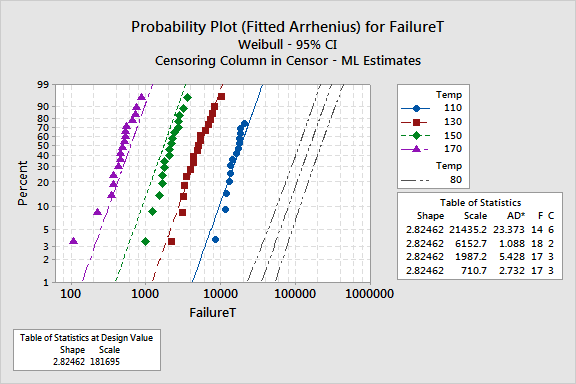
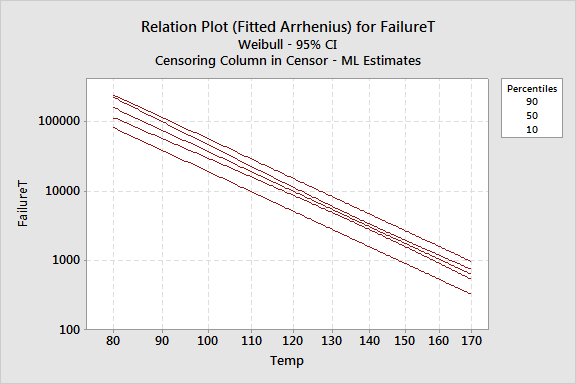
From the Regression Table, you get the coefficients for the regression model. For a Weibull distribution, this model describes the relationship between temperature and failure time for the insulation:

Loge (failure time) = -15.1874 + 0.83072 (ArrTemp) + 1/2.8246 ep

where ep = the pth percentile of the standard extreme value distribution

ArrTemp =

     11604.83        

     Temp + 273.16

The Table of Percentiles displays the 50th percentiles for the temperatures that you entered. The 50th percentile is a good estimate of how long the insulation will last in the field. At 80° C, the insulation lasts about 159,584.5 hours, or 18.20 years; at 100° C, the insulation lasts about 36,948.57 hours, or 4.21 years.

With the relation plot, you can look at the distribution of failure times for each temperature - in this case, the 10th, 50th, and 90th percentiles.

The probability plot based on the fitted model can help you determine whether the distribution, transformation, and assumption of equal shape (Weibull) at each level of the accelerating variable are appropriate. In this case, the points fit the lines adequately, thereby verifying that the assumptions of the model are appropriate for the accelerating variable levels.