Example of Parametric Growth Curve
main topic      interpreting results      session command     see also 

You want to estimate the replacement rate of a certain valve on a fleet of 24 diesel engines.

1    Open the worksheet VSEAT.MTW.

2    Choose Stat > Reliability/Survival > Repairable System Analysis > Parametric Growth Curve.

3    In Variable/Start variables, enter Days.

4    In System ID, enter ID.

5    Click OK.

Session window output

Parametric Growth Curve: Days

 

 

System:  ID

 

Model: Power-Law Process

Estimation Method: Maximum Likelihood

 

 

Parameter Estimates

 

                     Standard    95% Normal CI

Parameter  Estimate     Error    Lower    Upper

Shape       4.00405     0.406  3.28239  4.88436

Scale       420.130    18.590  385.229  458.193

 

 

Test for Equal Shape Parameters

Bartlett’s Modified Likelihood Ratio Chi-Square

 

Test Statistic  23.62

P-Value         0.425

DF                 23

 

 

Trend Tests

 

                   MIL-Hdbk-189        Laplace’s

                TTT-based  Pooled  TTT-based  Pooled  Anderson-Darling

Test Statistic      34.73   33.20       9.13    5.73             50.59

P-Value             0.000   0.000      0.000   0.000             0.000

DF                    142      96

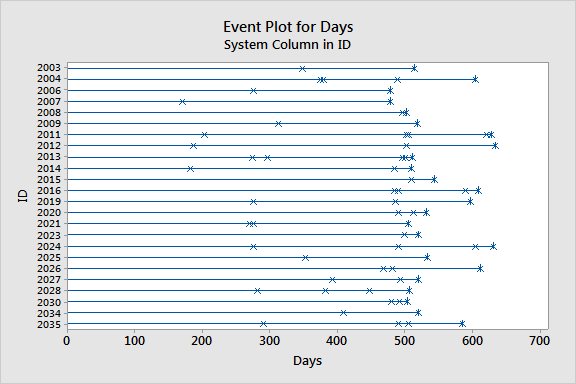
Graph window output

Interpreting the results

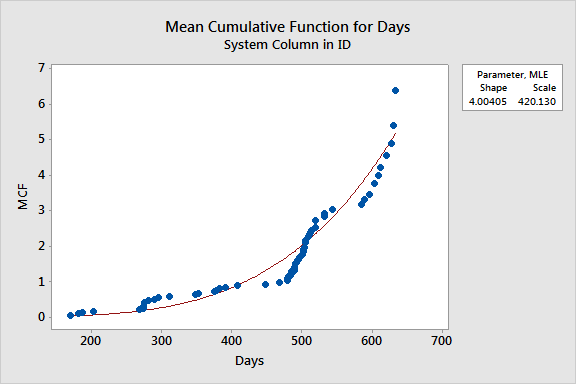
The estimate of the shape (4.004) is greater than 1, indicating that the failure rate is increasing. You can be 95% confident that the interval (3.282, 4.884) contains the true shape.

The test for equal shape parameters indicates that there is not enough evidence to say that the systems come from populations with different shapes (P-Value = 0.425). The pooled estimate of the shape is valid.

The tests for trend are all significant (P-Value = 0.000). This means that there is enough evidence to reject the null hypothesis that there is no trend in your data. You can conclude that the increasing trend is significant.

The event plot seems to show a pattern of failures that become more frequent as time goes on.

The plot of the MCF versus time shows a curve that is concave up. This plot is consistent with a shape that is greater than one, or a system that is deteriorating.