Example of a 1-Sample Equivalence Test
main topic     interpreting results     session command     see also 

You conduct an experiment on a new way to seal potato chip bags. You want to ensure that the force required to open the bags is within 10% of the target value of 4.2 N (Newtons). You collect 28 bags that are sealed using the new method and test the force required to open them.  

1    Open the worksheet SNACKBAGS.MTW.

2    Choose Stat > Equivalence Tests > 1-Sample.

3    Choose Sample in a column.

4    In Sample, enter Force.

5    In Target, enter 4.2.

6    From What do you want to determine, choose Lower limit < test mean - target < upper limit.

7    In Lower limit, enter -0.1 and in Upper limit enter 0.1.

8    Check Multiply by target.

9    Click OK.

Session window output

One-Sample Equivalence Test: Force

 

 

Method

 

Target = 4.2

Lower equivalence limit = -0.1 × target = -0.42

Upper equivalence limit = 0.1 × target = 0.42

 

 

Descriptive Statistics

 

Variable   N    Mean    StDev  SE Mean

Force     28  4.4850  0.73188  0.13831

 

 

Difference: Mean(Force) - Target

 

Difference       SE     95% CI     Equivalence Interval

   0.28500  0.13831  (0, 0.52059)      (-0.42, 0.42)

 

CI is not within the equivalence interval. Cannot claim equivalence.

 

 

Test

 

Null hypothesis:         Difference ≤ -0.42 or Difference ≥ 0.42

Alternative hypothesis:  -0.42 < Difference < 0.42

α level:                 0.05

 

Null Hypothesis     DF   T-Value  P-Value

Difference ≤ -0.42  27    5.0972    0.000

Difference ≥ 0.42   27  -0.97605    0.169

 

The greater of the two P-Values is 0.169. Cannot claim equivalence.

Graph window output

Interpreting the results

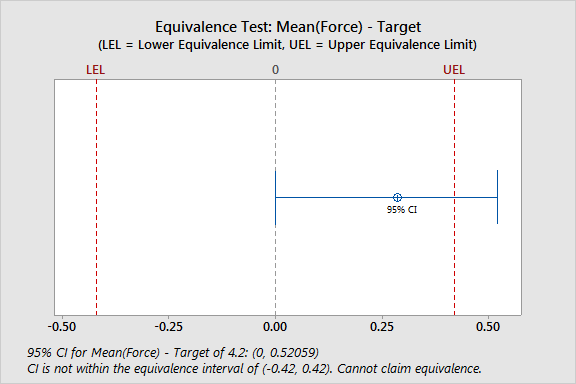
For the snack bag data, the confidence interval for the difference is not completely within the equivalence interval. Thus you cannot conclude that the force that is required to open the new bags is equivalent to the target of 4.2 N.