Example of an equivalence test with paired data
main topic     interpreting results     session command     see also 

You developed a new cleaning solution for contact lenses. You want to verify that your new solution cleans lenses as well as the leading brand. You have 14 participants wear contact lenses for a day, and then clean the lenses. Each participant cleans one lens in your solution and the other lens in the leading brand. By pairing the observations, you reduce the amount of variability that is caused by differences between participants. Finally, you assess the cleanliness of each lens by measuring the angle of contact for a drop of fluid on the lens. The angle of contact is affected by film or deposits on the lens.

1    Open the worksheet CONTACTLENS.MTW.

2    Choose Stat > Equivalence Tests > Paired.

3    In Test sample, enter New.

4    In Reference sample, enter 'Leading Brand'.

5    From Hypothesis about, choose Test mean - reference mean.

6    From What do you want to determine, choose Lower limit < test mean - reference mean < upper limit.

7    In Lower limit, enter -0.5 and in Upper limit, enter 0.5.

8    Click OK.

Session window output

Equivalence Test with Paired Data: New, Leading Brand

 

 

Method

 

Test mean = mean of New

Reference mean = mean of Leading Brand

 

 

Descriptive Statistics

 

Variable        N    Mean   StDev  SE Mean

New            14  88.604  1.5578  0.41634

Leading Brand  14  88.724  1.5907  0.42514

 

 

Difference: Mean(New) - Mean(Leading Brand)

 

Difference    StDev       SE         95% CI         Equivalence Interval

  -0.11929  0.42324  0.11312  (-0.31960, 0.081034)       (-0.5, 0.5)

 

CI is within the equivalence interval. Can claim equivalence.

 

 

Test

 

Null hypothesis:         Difference ≤ -0.5 or Difference ≥ 0.5

Alternative hypothesis:  -0.5 < Difference < 0.5

α level:                 0.05

 

Null Hypothesis    DF  T-Value  P-Value

Difference ≤ -0.5  13   3.3657    0.003

Difference ≥ 0.5   13  -5.4748    0.000

 

The greater of the two P-Values is 0.003. Can claim equivalence.

Graph window output

Interpreting the results

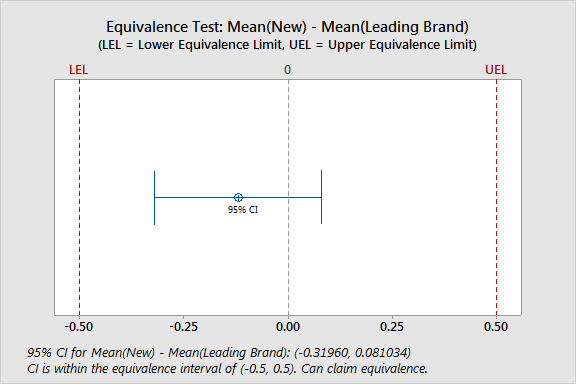
For the contact lens data, the confidence interval for the difference is completely within the equivalence interval. Thus you can conclude that both cleaning solutions are equally effective at cleaning contact lenses.