Example of partial least squares regression
main topic      interpreting results      session command      see also 

You are a wine producer who wants to know how the chemical composition of your wine relates to sensory evaluations. You have 37 Pinot Noir wine samples, each described by 17 elemental concentrations (Cd, Mo, Mn, Ni, Cu, Al, Ba, Cr, Sr, Pb, B, Mg, Si, Na, Ca, P, K) and a score on the wine's aroma from a panel of judges. You want to predict the aroma score from the 17 elements and determine that PLS is an appropriate technique because the ratio of samples to predictors is low. Data are from [12]. You want to include all elements (Cd-K) and all two-way interactions that include Cd in the model.

1    Open the worksheet WINEAROMA.MTW.

2    Choose Stat > Regression > Partial Least Squares.

3    In Responses, enter Aroma.

4    In Model, enter Cd-K Cd*Mo Cd*Mn Cd*Ni Cd*Cu Cd*Al Cd*Ba Cd*Cr Cd*Sr Cd*Pb Cd*B Cd*Mg Cd*Si Cd*Na Cd*Ca Cd*P Cd*K.

5    Click Options.

6    Under Cross-Validation, choose Leave-one-out. Click OK.

7    Click Graphs, then check Model selection plot, Response plot, Std Coefficient plot, Distance plot, Residual versus leverage, and Loading plot. Uncheck Coefficient plot.

8    Click OK in each dialog box.

Session window output

PLS Regression: Aroma versus Cd, Mo, Mn, Ni, Cu, Al, Ba, Cr, Sr, Pb, B, Mg, Si, Na, Ca, P, K

 

 

Method

 

Cross-validation                Leave-one-out

Components to evaluate          Set

Number of components evaluated  10

Number of components selected   4

 

 

Analysis of Variance for Aroma

 

Source          DF       SS       MS      F      P

Regression       4  34.5514  8.63784  41.55  0.000

Residual Error  32   6.6519  0.20787

Total           36  41.2032

 

 

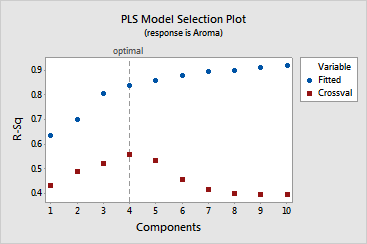
Model Selection and Validation for Aroma

 

Components  X Variance    Error      R-Sq    PRESS  R-Sq (pred)

         1    0.158849  14.9389  0.637435  23.3439     0.433444

         2    0.442267  12.2966  0.701564  21.0936     0.488060

         3    0.522977   7.9761  0.806420  19.6136     0.523978

         4    0.594546   6.6519  0.838559  18.1683     0.559056

         5               5.8530  0.857948  19.2675     0.532379

         6               5.0123  0.878352  22.3739     0.456988

         7               4.3109  0.895374  24.0041     0.417421

         8               4.0866  0.900818  24.7736     0.398747

         9               3.5886  0.912904  24.9090     0.395460

        10               3.2750  0.920516  24.8293     0.397395

Graph window output

Interpreting the results

Session window output

·    The Method table indicates the number of components Minitab evaluated and the number of components selected as the optimal model. The optimal model is defined as the model with the highest predicted R2. Minitab selected the four-component model as the optimal model, with a predicted R2 of 0.56.

·    Minitab displays one Analysis of Variance table per response based on the optimal model. The p-value for aroma is 0.000, which is less than an alpha of 0.05, providing sufficient evidence that the four-component model is significant.

·    Use the Model Selection and Validation table to select the optimal number of components for your model. Depending on your data or field of study, you may determine that a model other than the one selected by cross-validation is more appropriate. The model with four components, which was selected by cross-validation, has an R2 of 83.8% and a predicted R2 of 55.9%.

·    The X-variance indicates the amount of variance in the predictors that is explained by the model. In this example, the four-component model explains 59.4% of the variance in the predictors.

Graph window output

·    The model selection plot is a graphical display of the Model Selection and Validation table. The vertical line indicates that the optimal model has four components. You can see that the predictive ability of all models with more than four components decreases significantly.

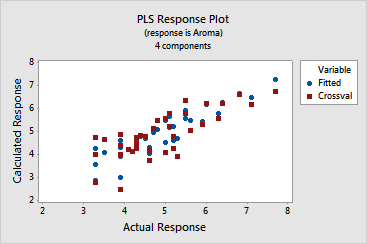
·    The response plot indicates that the model fits the data adequately because the points are in a linear pattern, from the bottom left-hand corner to the top right-hand corner. Although there are differences between the fitted and cross-validated fitted responses, none are severe enough to indicate an extreme leverage point.

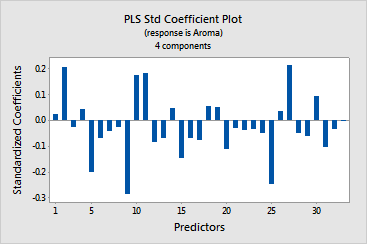
·    The coefficient plot displays the standardized coefficients for the predictors. You can use this plot to interpret the magnitude and sign of the coefficients. The elements Mo, Cu, Sr, Pb, B, Ca, Cd*Sr, Cd*B have the largest standardized coefficients and the biggest impact on aroma. The elements Mo, Pb, B, and Cd*B are positively related to aroma, while Cu, Sr, Ca, and Cd*Sr are negatively related.

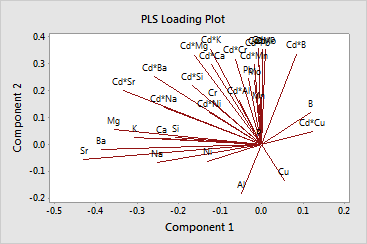
·    The loading plot compares the relative influence of the predictors on the response. In this example, Cu and Ni have very short lines, indicating that they have low x-loadings and are not related to aroma. The elements Sr, Mg, and Ba have long lines, indicating that they have higher loadings and are more related to aroma.

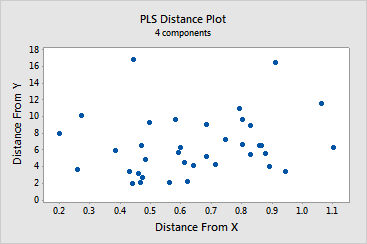
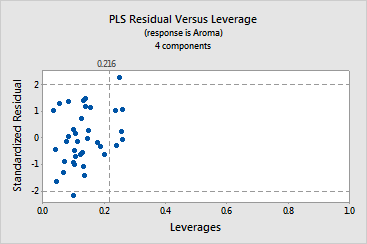
·    The distance plot and the residual versus leverage plot display outliers and leverages. By brushing the distance plot, you can see that compared to the rest of the data:

-    observations 14 and 32 have a greater distance value on the y-axis

-    observations in rows 1 and 37 have greater distance value on the x-axis

The residual versus leverage plot shows that:

-    observation 3 is an outlier because it is outside the horizontal reference lines

-    observations 5, 12, 14, 23, and 37 have extreme leverage values because they are to the right of the vertical reference line