Example of an overlaid contour plot for a Poisson regression model
main topic     interpreting results     session command     see also  

One product that a company makes are molded resin parts. The company knows that contamination in pipes and abrasions during transfer through hoses can lead to discolored streaks in the final product. A larger screw passes the pellets through the hoses faster. With a new type of resin pellet, the company decides to collect data on these discoloration defects to learn about the best way to transfer pellets.

1    Open the worksheet ResinDefects.MTW.

2    Choose Stat > Regression > Poisson Regression > Fit Poisson Model.

3    In Response, enter 'Discoloration Defects'.

4    In Continuous predictors, enter 'Hours Since Cleanse' and Temperature.

5    In Categorical predictors, enter 'Size of Screw'.

6    Click Model.

7    In Predictors, select Temperature and 'Size of Screw'.

8    For Interactions through order, choose 2.

9    Next to Interactions through order, click Add.

10  Click OK in both dialog boxes.

11  To recall the last dialog box, press [Ctrl]+[E].

12  In Response, enter 'Clump Defects'.

13  Click Model.

14  In Terms in the model, double-click 'Hours Since Cleanse' to remove the term from the model.

15  Click OK in both dialog boxes.

14  Choose Stat > Regression > Poisson Regression > Response Optimizer.

15  For Clump defects, choose Minimize.

16  For Discoloration Defects, choose Minimize.

17  Click Setup. Complete the Target and Upper columns of the table as shown below, then click OK.

Response

Target

Upper

Clump Defects

0

17

Discoloration Defects

0

75

18  Click Options. Complete the Constraint, Hold Value, Lower, and Upper columns of the table as shown below.

 

Variable

Constraints

Hold Value

Lower

Upper

Hours Since Cleanse

Constrain to region

 

3

8

Temperature

No Constraints

 

 

 

Size of Screw

Hold at value

large

 

 

19    Click OK in each dialog box.

Session Window Output

Response Optimization: Clump Defects, Discoloration Defects

 

 

Parameters

 

Response               Goal     Lower  Target  Upper  Weight  Importance

Clump Defects          Minimum              0     17       1           1

Discoloration Defects  Minimum              0     75       1           1

 

 

Variable Ranges

 

Variable             Values

Hours Since Cleanse  (3, 8)

Temperature          (80, 215)

Size of Screw        large

 

 

Solution

 

          Hours                            Clump  Discoloration

          Since                 Size of  Defects        Defects     Composite

Solution  Cleanse  Temperature  Screw        Fit            Fit  Desirability

1         3        122.273      large    14.7823        68.5972      0.105531

 

 

Multiple Response Prediction

 

Variable             Setting

Hours Since Cleanse  3

Temperature          122.273

Size of Screw        large

 

 

Response                 Fit  SE Fit      95% CI

Clump Defects          14.78    1.03  (12.89, 16.96)

Discoloration Defects  68.60    2.11  (64.58, 72.87)

Graph Window Output

Interpreting the results

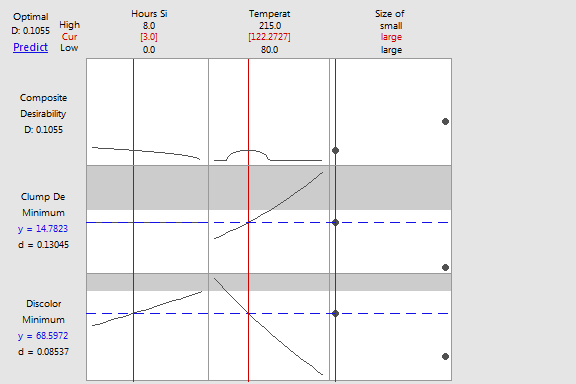
The combined or composite desirability of these two responses is 0.1055. The settings in the optimizer do not result in the highest composite desirability because of the constraints. The constraints make the solution more practical. Because discoloration defects increase with time and time is not in the model for clump defects, the highest composite desirability is always when Hours Since Cleanse is 0. Also, both types of defects are higher when the large screw transfers the pellets faster than the small screw, so the highest composite desirability is always when Size of Screw is small. The constraints make the solution more practical because the prediction shows that the process achieves the limits for the average numbers of defects for the faster transfer rate for at least 3 hours.

If you want to adjust the factor settings of this initial solution, you can use the plot. Move the vertical bars to change the factor settings and see how the individual desirability (d) of the responses and the composite desirability change. For example, you can move the red line for temperature to find that the prediction for the number of discoloration defects is less than the limit for the average number of defects when Temperature is about 147.

The response optimizer uses model equations. Ensure that your models are adequate before you interpret the results.