Example of a Poisson regression
main topic     interpreting results     session command     see also 

A manufacturer produces molded resin parts. Contamination in hoses and abrasions to resin pellets can lead to discolored streaks in the final product. Higher temperatures and faster rates of transfer can cause pellets to clump together. Clumps can be difficult to move through hoses and into molds. The company collects data on the number of defects per hour.

1    Open the worksheet ResinDefects.MTW.

2    Choose Stat > Regression > Poisson Regression > Fit Poisson Model.

3    In Response enter Discoloration Defects.

4    In Continuous Predictors enter Hours Since Cleanse and Temperature.

5    In Categorical Predictors enter Size of Screw.

6    Click Graphs.

7    In Residuals for Plots, choose Standardized.

8    Under Residual Plots, choose Four in One.

9    Click OK in each dialog box.

Session window output

 

Poisson Regression Analysis: Discoloratio versus Hours Since , Temperature, Size of Scre

 

 

Method

 

Link function                 Natural log

Categorical predictor coding  (1, 0)

Rows used                     36

 

 

Deviance Table

 

Source                 DF  Adj Dev  Adj Mean  Chi-Square  P-Value

Regression              3   56.670   18.8900       56.67    0.000

  Hours Since Cleanse   1    4.744    4.7444        4.74    0.029

  Temperature           1   38.800   38.8000       38.80    0.000

  Size of Screw         1   13.126   13.1256       13.13    0.000

Error                  32   31.607    0.9877

Total                  35   88.277

 

 

Model Summary

 

Deviance   Deviance

    R-Sq  R-Sq(adj)     AIC

  64.20%     60.80%  253.29

 

 

Coefficients

 

Term                      Coef   SE Coef   VIF

Constant                4.3982    0.0628

Hours Since Cleanse    0.01798   0.00826  1.00

Temperature          -0.001974  0.000318  1.00

Size of Screw

  small                -0.1546    0.0427  1.00

 

 

Regression Equation

 

Discoloration Defects  =  exp(Y')

 

 

Size of

Screw

large    Y' = 4.398 + 0.01798 Hours Since Cleanse - 0.001974 Temperature

 

small    Y' = 4.244 + 0.01798 Hours Since Cleanse - 0.001974 Temperature

 

 

Goodness-of-Fit Tests

 

Test      DF  Estimate     Mean  Chi-Square  P-Value

Deviance  32  31.60722  0.98773       31.61    0.486

Pearson   32  31.26713  0.97710       31.27    0.503

 

 

Fits and Diagnostics for Unusual Observations

 

     Discoloration

Obs        Defects    Fit  Resid  Std Resid

 33          43.00  58.18  -2.09      -2.18  R

 

R  Large residual

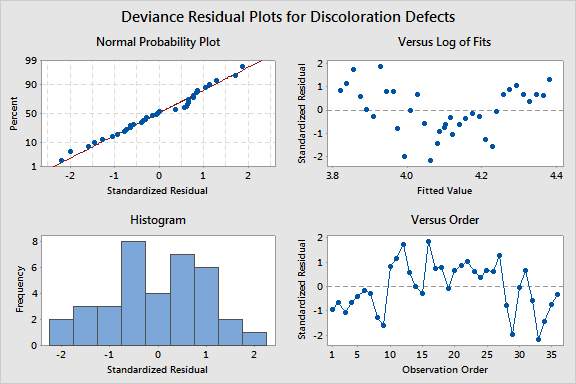
Interpreting the results

Session window output

·    The p-value for the regression model in the Analysis of Deviance table (0.000) shows that the model estimated by the regression procedure is significant at an a-level of 0.05. This indicates that at least one coefficient is different from zero.

·    The deviance R2 value indicates that the predictors explain 64.20% of the variance in the number of discolorations. The adjusted deviance R2  is 60.80%, which accounts for the number of predictors in the model. Use these values to compare this model to other models.

·    The Akaike Information Criterion (AIC) value is 253.29. Use the AIC to compare different models. The smaller the AIC, the better.

·    The coefficient for Hours Since Cleanse is 0.01798. Because the model uses the natural log link function and the coefficient is small, the coefficient indicates that the number of discolorations increases by about 1.8% each hour. See Interpreting the parameter estimates for more details.

·    One observation has a standardized residual less than -2. This point is not fit well by the model. Because the residuals show that the model is inadequate, you cannot evaluate whether the points are unusual yet.

Graph window output

·    The normal probability plot shows an approximately linear pattern consistent with a normal distribution. To investigate individual points, brush the graph.

·    The plot of the residuals versus the fitted values shows a distinct curve. This pattern indicates the model is inadequate. For these data, the pattern is because the size of the screw and the temperature interact but the interaction term is not in the model. The results are not reliable until you add the interaction term and the residual plots are satisfactory.

·    On the histogram, no residuals look unusual. Three residuals are in bins that include -2 and 2.  You can verify that one of the residuals is less than -2 on the other residual plots.

·    The plot of the residuals versus order begins with 9 negative residuals. The middle portion of the residuals tends to be higher than the residuals at the beginning and end of the data set. For these data, the pattern is also because of the missing interaction. The missing interaction looks like a time effect because the data were not collected in a random order.

See Checking your model and Identifying outliers for more information about residual plots.