Example of Forecasting with ARIMA
main topic     interpreting results     session command     see also 

In the example of fitting an ARIMA model, you found that an AR(1) model with a twelfth seasonal difference gave a good fit to the food sector employment data. You now use this fit to predict employment for the next 12 months.

Step 1: Refit the ARIMA model without displaying the acf and pacf of the residuals

1    Perform steps 1- 4 of Example of ARIMA.

Step 2: Display a time series plot

1    Click Graphs. Check Time series plot. Click OK.

Step 3: Generate the forecasts

1    Click Forecast. In Lead, enter 12. Click OK in each dialog box.

Session window output

ARIMA Model: Food

 

 

Estimates at each iteration

 

Iteration      SSE   Parameters

        0  95.2343  0.100  0.847

        1  77.5568  0.250  0.702

        2  64.5317  0.400  0.556

        3  56.1578  0.550  0.410

        4  52.4345  0.700  0.261

        5  52.2226  0.733  0.216

        6  52.2100  0.741  0.203

        7  52.2092  0.743  0.201

        8  52.2092  0.743  0.200

        9  52.2092  0.743  0.200

 

Relative change in each estimate less than 0.0010

 

 

Final Estimates of Parameters

 

Type        Coef  SE Coef     T      P

AR   1    0.7434   0.1001  7.42  0.000

Constant  0.1996   0.1520  1.31  0.196

 

 

Differencing: 0 regular, 1 seasonal of order 12

Number of observations:  Original series 60, after differencing 48

Residuals:    SS =  51.0364 (backforecasts excluded)

              MS =  1.1095  DF = 46

 

 

Modified Box-Pierce (Ljung-Box) Chi-Square statistic

 

Lag            12     24     36  48

Chi-Square   11.3   19.1   27.7   *

DF             10     22     34   *

P-Value     0.338  0.641  0.768   *

 

 

Forecasts from period 60

 

                     95% Limits

Period  Forecast    Lower    Upper  Actual

    61   56.4121  54.3472  58.4770

    62   55.5981  53.0251  58.1711

    63   55.8390  53.0243  58.6537

    64   55.4207  52.4809  58.3605

    65   55.8328  52.8261  58.8394

    66   59.0674  56.0244  62.1104

    67   69.0188  65.9559  72.0817

    68   74.1827  71.1089  77.2565

    69   76.3558  73.2760  79.4357

    70   67.2359  64.1527  70.3191

    71   61.3210  58.2360  64.4060

    72   58.5100  55.4240  61.5960

Graph window output

Interpreting the results

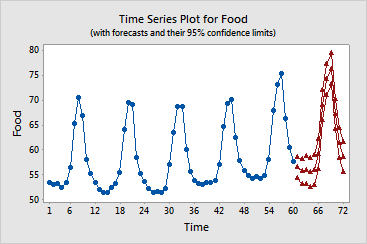
ARIMA gives forecasts, with 95% confidence limits, using the AR(1) model in both the Session window and a Graph window. The seasonality dominates the forecast profile for the next 12 months with the forecast values being slightly higher than for the previous 12 months.