Standard deviation
The most common measure of dispersion, or how spread out the data are
from the mean. While the range estimates the spread of the data by subtracting
the minimum value from the maximum value, the standard deviation roughly
estimates the "average" distance of the individual observations
from the mean. The greater the standard deviation, the greater the spread
in the data.
Standard deviation can be used as a preliminary benchmark for estimating
the overall variation of a process. For example, administrators track
the discharge time for patients treated in the emergency departments of
two hospitals. Although the average discharge times are about the same
(35 minutes), the standard deviations are significantly different.
|
|
|
|
|
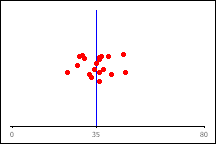
Hospital 1 The
standard deviation is about 6. On average, a patient's discharge time
deviates from the mean (blue line) by about 6 minutes. |
|
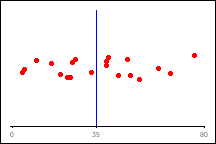
Hospital 2 The
standard deviation is about 20. On average, a patient's discharge time
deviates from the mean (blue line) by about 20 minutes. |
The standard deviation is calculated by taking the positive square root
of the variance, another measure of data dispersion. Standard deviation
is often more convenient and intuitive to work with, however, because
it uses the same units as the data. For example, if a machine part is
weighed in grams, the standard deviation of its weight is also calculated
in grams, while its variance is calculated in grams2.
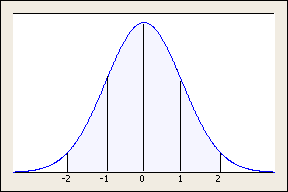
In a normal (bell-shaped) distribution, successive
standard deviations from the mean provide useful benchmarks for estimating
the percentage of data observations.
|
|
About 95% of the observations fall within 2 standard deviations of the
mean, shown by the blue shaded area.
About 68% of the observations fall within 1 standard deviation from
the mean (-1 to +1), and about 99.7% of the observations would fall within
3 standard deviations of the mean (-3 to +3).
|
The symbol s
(sigma) is
often used to represent the standard
deviation of a population, while s
is used to represent the standard
deviation of a sample.
Variation that is not random or natural to a process is often referred
to as noise.


