使用概率图来评估数据是否服从正态分布。概率图包括：

·    点 - 顺序数据集的对应概率的估计百分位数。

·    中线 - 基于极大似然参数估计的分布的预期百分位数。如果分布是数据的良好拟合，这些点将形成一条直线。

·    左侧线 - 通过连接百分位数的置信区间的下限形成。同样，通过连接百分位数的置信区间上限，可形成右侧线。如果分布是良好的拟合，这些点将在这些边界之内。

·    带有对应 p 值的 Anderson-Darling 检验统计量 - 用于评估数据是否服从某一分布。

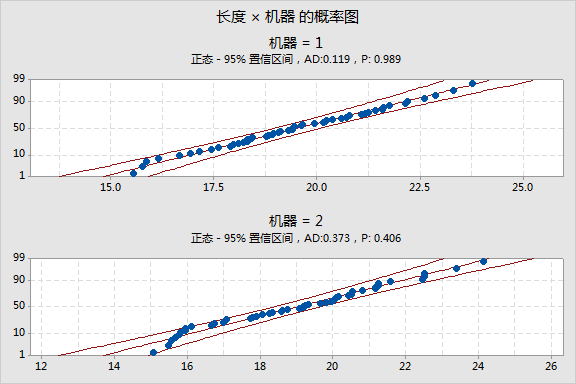
对于插销数据：

·    机器 1 的概率图显示点的位置接近于中线，并且在置信区间以内。Anderson-Darling 统计量 (0.119) 和 p 值 (0.989) 暗示正态分布是良好拟合的。

·    机器 2 的概率图显示点的位置接近于中线，并且在置信区间以内。Anderson-Darling 统计量 (0.373) 和 p 值 (0.406) 暗示正态分布是良好拟合的。