主题 解释结果 会话命令 另请参见
您要确定包含一种新药成分的药丸的保质期。该成分在药丸中的浓度随着时间而降低。您想要确定药丸何时达到预期浓度的 90%。
您创建了 5 批药品,并在 9 个不同的时间从每批中抽出一粒药丸进行检验。您在创建稳定性研究工作表示例中为此研究创建了一个数据收集工作表。
1 打开工作表“保质期.MTW”。
2 选择统计 > 回归 > 稳定性研究 > 稳定性研究。
3 在响应中,输入药物含量。
4 在时间中,输入月。
5 在批次中输入批次。
6 在规格下限中,键入 90。
7 单击图形。
8 在保质期图下方的第二个下拉列表中,选择单个批次不生成图形。
9 在残差图下,选择四合一。
10 在每个对话框中单击确定。
会话窗口输出
稳定性研究: 药物% 与 月份,批次
方法
未使用的行 5
因子信息
因子 类型 水平数 水平数 批次 固定 5 1, 2, 3, 4, 5
模型选择,α = 0.25
来源 自由度 Seq SS Seq MS F 值 P 值 月份 1 122.460 122.460 345.93 0.000 批次 4 2.587 0.647 1.83 0.150 月份*批次 4 3.850 0.962 2.72 0.048 误差 30 10.620 0.354 合计 39 139.516
选定模型中的项: 月份, 批次, 月份*批次
模型汇总
R-sq(调 S R-sq 整) R-sq(预测) 0.594983 92.39% 90.10% 85.22%
系数
方差膨 项 系数 系数标准误 T 值 P 值 胀因子 常量 100.085 0.143 701.82 0.000 月份 -0.13633 0.00769 -17.74 0.000 1.07 批次 1 -0.232 0.292 -0.80 0.432 3.85 2 0.068 0.292 0.23 0.818 3.85 3 0.394 0.275 1.43 0.162 3.41 4 -0.317 0.292 -1.08 0.287 3.85 5 0.088 0.275 0.32 0.752 * 月份*批次 1 0.0454 0.0164 2.76 0.010 4.52 2 -0.0241 0.0164 -1.47 0.152 4.52 3 -0.0267 0.0136 -1.96 0.060 3.65 4 0.0014 0.0164 0.08 0.935 4.52 5 0.0040 0.0136 0.30 0.769 *
回归方程
批次 1 药物% = 99.853 - 0.0909 月份
2 药物% = 100.153 - 0.1605 月份
3 药物% = 100.479 - 0.1630 月份
4 药物% = 99.769 - 0.1350 月份
5 药物% = 100.173 - 0.1323 月份
异常观测值的拟合和诊断
观测值 药物% 拟合值 残差 标准残差 11 98.001 99.190 -1.189 -2.21 R 43 92.242 92.655 -0.413 -1.47 X 44 94.069 93.823 0.246 0.87 X
R 残差大 X 异常 X
估计稳定期
规格下限 = 90 稳定期 = 您可以 95% 确信至少 50% 的响应高于规格下限的时间期间
批次 稳定期 1 83.552 2 54.790 3 57.492 4 60.898 5 66.854 整体 54.790 |
图形窗口输出
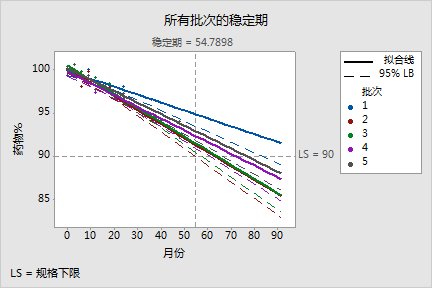
对于药丸数据,月份和批次交互作用的 p 值(月份*批次)为 0.048。由于该 p 值小于 0.25 a 水平,因而无法减少模型。
月及月和批次的交互作用均非常显著。因此,每个批次的回归方程具有不同的截距和斜率。批次 3 的斜率最陡,为 -0.1630,说明每个月批次 3 的药物浓度(药物含量)下降 0.163 个百分点。批次 4 的截距最小,为 99.769,说明批次 4 在时间 0 的浓度最低。
Minitab 显示每个批次的保质期估计值。最短的保质期估计值为 54.79 个月,因此产品的总体保质期估计在 54.79 个月。
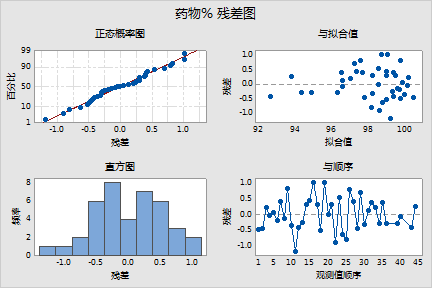
残差正态分布似乎较为合理并围绕着零随机分散。残差与拟合值图右侧的点比左侧多。之所以形成此模式,是因为早些时候当药物浓度较高时,在研究中收集的观测值较多。