主题 解释结果 会话命令 另请参见
您要使用过去的就业数据预测食品加工业的就业情况。为此,您要使用 ARIMA,但首先使用自相关以帮助确认有希望采用的模型。由于数据显示出一个 12 月强季节性分量,因此您在滞后 12 处执行差分以实现平稳性并查看差分序列的自相关。这些数据中可能会存在某种长期趋势,但其量与季节性分量相比似乎太小。如果趋势较大,可以考虑在滞后 1 处执行另一个差分以实现平稳性。
1 打开工作表“服务处所.MTW”。
2 选择统计 > 时间序列 > 差分。
3 在序列项下,输入食品。
4 在将差分存储在中,输入食品2。
5 在滞后中,输入 12。单击确定。
6 选择 统计 > 时间序列 > 自相关。
7 在序列中,输入食品2。单击确定。
会话窗口输出
自相关函数: 食品 2
滞后 (Lag) ACF T LBQ 1 0.701388 4.86 25.12 2 0.512266 2.52 38.81 3 0.366882 1.60 45.99 4 0.310364 1.29 51.24 5 0.234743 0.94 54.32 6 0.173069 0.68 56.03 7 0.162046 0.63 57.57 8 0.170051 0.66 59.30 9 0.322438 1.24 65.70 10 0.252774 0.94 69.74 11 0.208020 0.76 72.54 12 0.150936 0.55 74.06
食品 2 的自相关 |
图形窗口输出
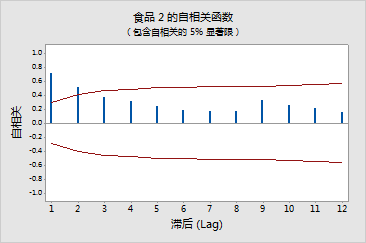
在会话窗口中,Minitab 显示自相关、关联 t 统计量和 Ljung-Box Q 统计量。由于未指定滞后长度,因此自相关对观测值数小于或等于 240 的序列使用默认长度 n/4。Minitab 生成自相关函数 (ACF),其中大约有 a = 0.05 临界带对应于“相关等于零”这一假设。
这些数据的 ACF 显示在滞后 1 和 2 处有较大的正峰值,且后续正相关消失得并不快。此模式在自回归过程中很典型。
要检验“所有滞后(直到滞后 6)的自相关为零”这一原假设,请参见检验自相关示例。