累积 DPU 图
DPU
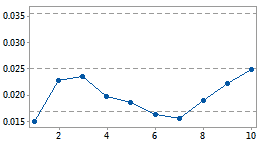
此能力研究未包含足够的样本来估计 DPU 均值。
样本
累积 DPU 图
DPU
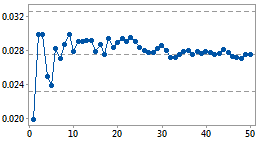
此能力研究包含了足够样本来估计 DPU 均值。
样本
在 Poisson 数据的能力分析中,此控制图可帮助验证收集的数据来自足够的样本,可计算出每观测单位缺陷数 (DPU) 的均值的稳定估计。此统计量是能力研究的核心,因此,如果没有足够的数据来估计 DPU 均值,分析将无法继续。
此图形针对顺序样本标绘了 DPU 均值,以显示当收集更多样本时估计值如何变化。当估计水平趋于一个稳定值时,可以认定已经收集了足够样本。该图还包含代表 DPU 均值的水平线(根据所有样本计算得出)及其置信上限和下限。
例如,您要通过计数每平方英尺的缺陷数来研究一台地毯编织机的能力。此值服从 Poisson 分布。您收集了 10 块地毯样本并生成下面第一个累积 DPU 图。但是,DPU 均值的估计尚未达到稳定值,因为 10 块地毯的样本数量太少。然后,您又收集了 50 块地毯样本并生成下面的第二个图形,它清楚表明 DPU 均值的估计已达到一个稳定值。这时可以认定 50 个样本能提供足够数据来进行您的能力研究,因此可以继续分析。
|
|
累积 DPU 图 |
|
|
DPU |
|
此能力研究未包含足够的样本来估计 DPU 均值。 |
|
|
样本 |
|
|
|
|
|
|
|
累积 DPU 图 |
|
|
DPU |
|
此能力研究包含了足够样本来估计 DPU 均值。 |
|
|
样本 |
|
| 品质管理 | 六西格玛 | 计量和实验 | ISO9001等体系 | IATF16949,VDA |
| Minitab帮助 | Minitab图形 | Minitab DOE | Minitab基础统计 | SPC,MSA,CPK等 |
| 华为内部资料 学习培训(汇总) | |
| 比亚迪,特斯拉,博世,丰田,大众等资料 | |
| 可靠性工程, 测试方法及标准 | |
| 8D报告案例、质量成本 | |
| 六西格玛、DFSS, 数据分析 | |
| APQP, PPAP, FMEA, MSA, SPC | |
| ISO9001, ISO14001, ISO45001等体系认证 | |
| 总去赌场为什么会输惨?数据分析告诉你 |