累积不良品率图
不良品率
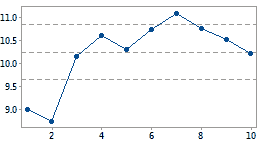
此能力研究未包含足够的样本来估计不良品率均值。
样本
累积不良品率图
不良品率
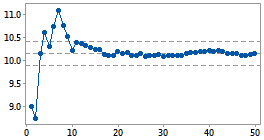
此能力研究包含了足够样本来估计不良品率均值。
样本
在二项数据的能力分析中,此图形可帮助验证收集的数据来自足够的样本,可计算过程中缺陷项目百分比(不良品率)的均值的稳定估计。此统计量是能力研究的核心,因此,如果没有足够的数据来估计不良品率均值,分析将无法继续。
此图形针对顺序样本标绘了不良品率均值,以显示当收集更多样本时估计值如何变化。当估计水平趋于一个稳定值时,可以认定已经收集了足够样本。该图还包含代表不良品率均值的水平线(根据所有样本计算得出)及其置信上限和下限。
例如,您要研究您公司的旷工情况,因此观测在随机的 10 天内的旷工员工百分比。因为旷工是一个二元条件(出勤或缺勤),所以使用二元能力分析来分析数据。输出包括下面的第一个累积不良品率图。10 个抽样的不良品率估计尚未稳定,因此必须收集更多样本以便继续分析。您使用来自 50 天的数据重复此调查,并生成下面的第二个累积不良品率图。它清楚表明不良品率的估计已达到一个稳定值。这时可以认定 50 个样本能提供足够数据来进行您的能力研究,因此可以继续分析。
|
|
累积不良品率图 |
|
|
不良品率 |
|
此能力研究未包含足够的样本来估计不良品率均值。 |
|
|
样本 |
|
|
|
|
|
|
|
累积不良品率图 |
|
|
不良品率 |
|
此能力研究包含了足够样本来估计不良品率均值。 |
|
|
样本 |
|