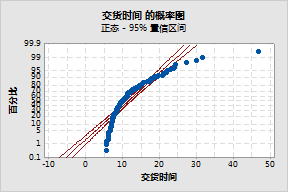
比萨饼送货时间向右偏斜,而且未呈正态分布。
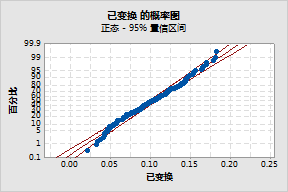
取倒数以使数据更服从正态分布。倒数是使用方程 Y = 1/X 来获得的。因此变换后的数据 = 1/送货时间。概率图显示变换后的数据更加符合正态分布。
许多分析都需要正态性假设。如果数据为非正态,有时您可以应用函数以使数据近乎正态,以便可以完成分析。
例如,假设您需要针对比萨饼送货所需的时间执行能力分析。尽管存在最小时间(下限),但可能没有最大时间(上限),因此数据可能会向右侧偏斜。
|
|
|
|
比萨饼送货时间向右偏斜,而且未呈正态分布。 |
取倒数以使数据更服从正态分布。倒数是使用方程 Y = 1/X 来获得的。因此变换后的数据 = 1/送货时间。概率图显示变换后的数据更加符合正态分布。 |
根据数据,存在许多不同的函数(如平方根、对数、幂、倒数或反正弦),可以应用这些函数来变换数据。在您不确定要尝试哪种变换时,Minitab 可以提供帮助。
Minitab 提供了两种数据变换方法:
Box-Cox 变换很容易理解,但是作用非常有限,而且通常找不到适合的变换。而且,此变换仅适用于正数据。
如果 Box-Cox 算法找不到合适的变换,请尝试 Johnson 变换(或假设数据服从非正态分布,并且使用其他分布,而不变换数据)。Johnson 变换函数较为复杂,但对于查找合适的变换而言功能非常强大。
|
注意 |
Box-Cox 变换利用数据位于子组中(当子组 > 1 时)这样一个事实;但 Johnson 变换不利用这个事实。这就是“子组内”分析只能使用 Box-Cox 变换的原因所在。 |