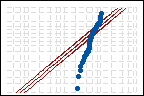
指数分布
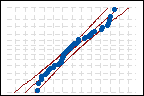
正态分布
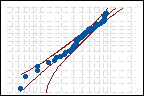
3 参数 Weibull 分布
Anderson-Darling 统计量 = 9.599
P 值 < 0.003
Anderson-Darling 统计量 = 0.641
p 值 = 0.089
Anderson-Darling 统计量 = 0.376
p 值 = 0.432
通过分析观测值与其模型中的预期值之间的差异,确定统计模型是否与数据拟合。对于连续数据,可以使用概率图直观评估拟合优度,也可以使用假设检验(如 Anderson-Darling 检验)以数量方式进行评估。对于类别数据,可以使用卡方检验或 Poisson 数据的 Minitab 拟合优度检验。Minitab 还将针对 Logistic 回归模型执行拟合优度检验。
拟合优度检验使用以下假设:
例如,您希望找到能为灯泡失效时间进行最佳建模的分布。对灯泡样本运行寿命试验,以观测其失效时间。可以使用 Minitab 的概率图来比较三种分布向数据提供的拟合优度。
|
指数分布 |
正态分布 |
3 参数 Weibull 分布 |
|
|
|
|
|
Anderson-Darling 统计量 = 9.599 P 值 < 0.003 |
Anderson-Darling 统计量 = 0.641 p 值 = 0.089 |
Anderson-Darling 统计量 = 0.376 p 值 = 0.432 |
指数分布的 p 值很低,足以拒绝良好拟合的原假设。当 Alpha 水平为 0.05 时,正态分布和 3 参数 Weibull 分布都提供了对数据的良好拟合。某些分析人员选择包含最高 p 值的分布,但包含不显著 p 值的任何分布都是可接受的。