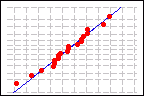
正态数据的概率图
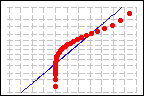
非正态数据的概率图
确定您绘制样本所基于的总体是否呈非正态分布的单样本假设检验。许多统计过程均依赖于总体正态性,且使用正态性检验确定否定此假设是不是分析中的重要步骤。正态性检验的原假设假定总体为正态分布。备择假设假定总体为非正态分布。要确定样本数据是否来自非正态总体,您可以从四种检验中进行选择。
您可以使用正态概率图来评估总体正态性,如果样本的总体呈正态分布,该图将根据您期望它们接近的值绘制顺序数据值。如果总体呈正态分布,绘制的点将大致形成一条直线。
|
正态数据的概率图 |
非正态数据的概率图 |
|
|
|
|
|
|
此检验是将样本数据的经验累积分布函数与假设数据呈正态分布时期望的分布进行比较。如果实测差异足够大,该检验将否定总体呈正态分布的原假设。
此检验通过计算数据与数据的正态分值之间的相关性来评估正态性。如果相关系数接近 1,则总体就很有可能呈正态分布。Ryan-Joiner 统计量可以评估这种相关性的强度;如果它未达到适当的临界值,您将否定总体呈正态分布的原假设。此检验类似于 Shapiro-Wilk 正态性检验。
此检验是将样本数据的经验累积分布函数与假设数据呈正态分布时期望的分布进行比较。如果实测差异足够大,该检验将否定总体呈正态分布的原假设。
如果这些检验的 p 值低于您选择的 a 水平,您可以否定原假设并断定总体呈非正态分布。
一种非正式的近似正态性检验,称为“粗笔检验”,常应用于概率图。想象有一支“粗笔”从拟合线上划过:如果它覆盖了图中的所有数据点,则数据可能为正态分布;如果图中的点距离拟合线很远以致粗笔边缘之外还有很多点,则数据可能为非正态分布。这种非正式的方法并不能代替正态性检验的统计推断,但它可以作为一种有用的快速直观评估方式。在下列图形中,将粗笔检验应用到了上面的概率图中。灰色带形就表示在拟合线上划的粗笔。
|
对正态数据的“粗笔检验” |
对非正态数据的“粗笔检验” |
|
|
|