方差

对离差的度量，离差是数据集或分布围绕其均值散布的程度。

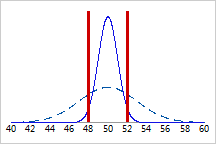
监视方差对于制造和质量行业必不可少，因为减小过程方差将提高精度并减小缺陷数。例如，一家工厂生产长度为 50mm 的木工钉，如果钉子的长度与目标值 50mm 之差在 2mm 之内，则钉子满足规格。工厂使用两种类型的机器生产钉子。两台机器都生产长度服从正态分布且平均长度为 50mm 的钉子。但是，每台机器生产的钉子具有不同的方差：机器 A（下面的虚线分布）所生产钉子的方差为 9mm2，机器 B（下面的实线分布）所产生钉子的方差为 1mm2。每台机器所生产钉子的长度分布相互重叠，还包括垂直的规格上限和下限：

机器 A 所生产钉子长度的方差大于机器 B 所生产钉子长度的方差。因此，机器 A 所生产的任何给定钉子在规格限之外的可能性都比机器 B 所生产的钉子大。

由于方差 (s2) 是量的平方，因此其单位也是平方单位，这在实际讨论中容易混淆。例如，在公共汽车站等待时间样本的均值为 15 分钟，方差为 9 分钟2。为避免这一混淆，通常以其平方根显示方差，即标准差 (s)，这是更直观的测量值。方差 9 分钟2 等效于标准差 3 分钟。