Tolerance interval plots contain the following:

·    A histogram to visualize the distribution of your sample data. Look at the central tendency, variation, and overall shape of the distribution. A histogram can help you confirm assumptions and guide further analysis.

·    Interval plots to visualize the sample mean along with the upper and/or lower bounds of the tolerance intervals. A vertical line at the end of the interval represents a bound while an arrow indicates there is no bound for that side of the interval.

Minitab uses an exact method to calculate the normal tolerance intervals.

·    A normal probability plot to help you determine whether your data follow a normal distribution. If your data are perfectly normal, then the data points on the probability plot form a straight line.

·    A table displaying the mean, standard deviation, the normal and nonparametric method tolerance intervals, and Anderson-Darling normality test values. The normality test evaluates the null hypothesis (H0) that the data follow a normal distribution. If the p-value for the test is less than your chosen a-level, then you must reject H0 and conclude that your data do not follow a normal distribution.

·    For the nonparametric method, Minitab calculates the achieved confidence level. This is the exact confidence level obtained from your sample. It will generally be greater than or equal to your desired confidence level, unless your sample size is too small.

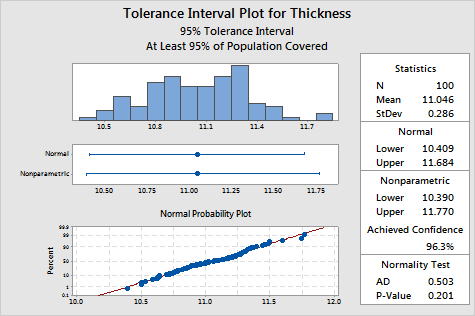
The normal probability plot shows that the points fall reasonably close to the reference line, which indicates that the data follow a normal distribution. The p-value for the Anderson-Darling normality test (bottom right) of the washer data is 0.201. This value is greater than the chosen a-level of 0.05. Thus, there is not enough evidence to suggest that the data do not follow a normal distribution. Use the normal method results.

The manufacturer is interested in the range that most washer thicknesses will fall in. The tolerance intervals contain this information. Because the data are normally distributed, the manufacturer is 95% confident that at least 95% of all washers produced will have thicknesses falling in the normal method interval [10.409 11.684].

The analyst compares this tolerance interval to a major client's washer specs [10 12]. Because the tolerance interval is contained within the client's requirements, the analyst concludes that current thickness variability is not excessive.