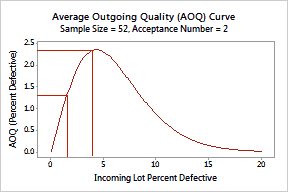
For example, you sample 52 rollers from a shipment of 500. If the actual % defective is 1.5%, the average outgoing quality is 1.28% defective.
By plotting the AOQ curve, the outgoing quality levels are evident.
Approximates the relationship between the quality of the incoming material and the quality of the outgoing material, assuming that rejected lots will be 100% inspected and defective items will be reworked and inspected again (rectifying inspection).
The average outgoing quality depends on the incoming quality, the probability that the lot will be accepted, and the sample and lot sizes.
|
|
For example, you sample 52 rollers from a shipment of 500. If the actual % defective is 1.5%, the average outgoing quality is 1.28% defective. By plotting the AOQ curve, the outgoing quality levels are evident. |
When incoming quality is very good, naturally outgoing quality is very good. When incoming quality is very bad, the entire lot is rejected; therefore the outgoing quality is also very good because the lot will be rejected and the bad parts won't get through.
When incoming quality is neither very good or very bad, the outgoing quality gets worse and the % defective in the outgoing level reaches a maximum known as the Average Outgoing Quality Limit (AOQL). In the example, at 4.29% defective, the outgoing quality level reaches its worst case average of 2.36% defective.
You can also compare AOQ curves to help choose the appropriate sampling plan.
|
|
In this case, the shift supervisor thinks sampling 52 rollers from 500 is too much. You can develop curves for various sample sizes and acceptance numbers to illustrate the increased risk to the outgoing quality levels. If the sample size is 35 (red line) and the %defective is 1.5%, the average outgoing quality is 1.37% defective.
|
Look at OC curves, AOQ curves, and ATI curves together when your corrective action for rejected lots is 100% inspection.