Use to examine the accuracy of a gage.
Bias examines the difference between the observed average measurement and a reference or master value. It answers the question: "How accurate is my gage when compared to a reference value?" Linearity examines how accurate your measurements are through the expected range of the measurements. It answers the question: "Does my gage have the same accuracy across all reference values?"
For example, a manufacturer wants to know if a thermometer is taking
accurate and consistent readings at five heat settings (202
To find out if the thermometer is taking biased measurements, subtract
the individual readings from the reference value. The bias values for
measurements taken at heat setting 202
|
Thermometer reading |
|
Actual temperature |
|
Bias |
|
The temperature readings at the 202 |
|
202.7 |
- |
202 |
= |
0.7 |
|
|
|
202.5 |
- |
202 |
= |
0.5 |
|
|
|
203.2 |
- |
202 |
= |
1.2 |
|
|
|
203.0 |
- |
202 |
= |
1.0 |
|
|
|
203.1 |
- |
202 |
= |
1.1 |
|
|
|
203.3 |
- |
202 |
= |
1.3 |
|
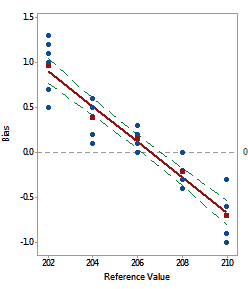
To interpret the linearity of the thermometer data, determine if the bias of the thermometer changes across the heat settings. If the data do not form a horizontal line on a scatterplot, linearity is present.
|
|
The scatterplot shows that bias changes as the heat settings increase. Temperatures for lower heat settings are higher than the actual temperatures, while readings for higher heat settings are lower than the actual temperatures. Because bias changes over the heat settings, linearity is present in this data. |
