These plots appear in the output for binomial capability analysis to help verify whether your data follow the binomial distribution. If they do not, binomial capability analysis is not appropriate for your data. Minitab generates a Rate of defectives plot when the subgroup sizes vary, and a Binomial plot when subgroup sizes are constant.
This chart helps you verify whether your data is binomial by checking the assumption that the probability of a defective item is constant. If your data violate this assumption, your capability analysis may be invalid.
This chart plots the percent of defective items in a subgroup (%Defective) against the subgroup's sample size. The center line equals the mean probability that an item is defective; the confidence bounds for the mean lie above and below the center line.
If your data fall randomly about the center line, you conclude the binomial distribution is a good fit for your data, and proceed with your analysis. If the points fall in a nonrandom pattern, the binomial distribution may not be appropriate for your data, and your capability analysis may not be valid.
|
|
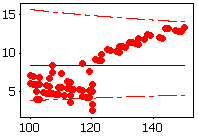
Rate of Defectives plot |
|
|
%Defective |
|
%Defective is correlated with sample sizes greater than 120. The data do not follow a binomial distribution. |
|
|
Sample size |
|
|
|
|
|
|
|
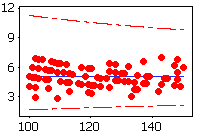
Rate of Defectives plot |
|
|
%Defective |
|
The points are scattered randomly around the center line. It is reasonable to assume the data come from a binomial population. |
|
|
Sample size |
|
This chart helps verify whether your data are binomial by plotting the expected number of defective items against the observed number of defective items. The diagonal line shows where the data would fall if they perfectly follow the binomial distribution. If the data stray significantly from this line, binomial capability analysis may be invalid.
|
|
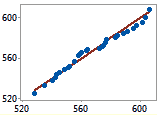
Binomial plot |
|
|
Expected Defectives |
|
The data points fall closely along the line. It is reasonable to assume the data comes from a binomial population. |
|
|
Observed Defectives |
|
