Continuous distribution

Describes the probabilities of the possible values of a continuous random variable. A continuous random variable is a random variable with a set of possible values (known as the range or support) that is infinite and uncountable. For example, the continuous normal distribution can describe the distribution of weight of adult males.

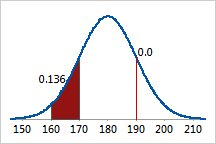
Probabilities of continuous random variables (X) are defined as the area under the curve of its distribution. Therefore, the only events that can have nonzero probabilities are those in which the random variable falls within a range of values. For example, you can calculate the probability that a man weighs between 160 and 170 pounds. The shaded region under the curve below represents this range, and the area of the shaded region equals the probability of this event. The area is 0.136; therefore, the probability that a man weighs between 160 and 170 pounds is 13.6%.

However, the probability that X is exactly equal to some value is always zero because the area under the curve above a single point, which has no width, is zero. For example, the probability that a man weighs exactly 190 pounds to infinite precision is zero. You could calculate a nonzero probability that a man weighs more than 190 pounds, or less than 190 pounds, or between 189.9 and 190.1 pounds, but the probability that he weighs exactly 190 pounds is zero.

The entire area under the curve equals 1.0.