Cumulative DPU plot
DPU
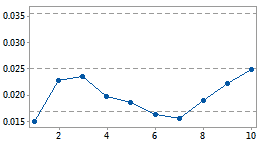
This capability study does not include enough samples to estimate mean DPU.
sample
Cumulative DPU plot
DPU
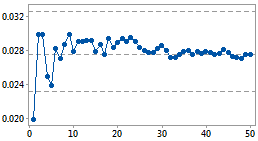
This capability study includes enough samples to estimate mean DPU.
sample
In capability analysis for Poisson data, this chart helps verify that you have collected data from enough samples to calculate a stable estimate of the mean number of defects per unit of observation (DPU). This statistic is central to the capability study, so without sufficient data to estimate mean DPU, the analysis cannot continue.
This graph plots the mean DPU against the ordered samples to show how the estimate changes as you collect more samples. You can conclude that you have collected enough samples when the estimate levels off to a stable value. The plot also includes horizontal lines to represent the mean DPU, calculated from all samples, and its upper and lower confidence bounds.
For example, you are studying the capability of a machine that weaves carpets by counting the number of defects per square foot. This value follows a Poisson distribution. You collect ten carpet samples and produce the first cumulative DPU plot below. However, the estimate of mean DPU has not yet reached a stable value because ten samples are too few. You then collect fifty samples and produce the second graph below, which clearly shows the estimate of mean DPU reaching a stable value. You conclude that fifty samples provide sufficient data to conduct your capability study, so you continue with the analysis.
|
|
Cumulative DPU plot |
|
|
DPU |
|
This capability study does not include enough samples to estimate mean DPU. |
|
|
sample |
|
|
|
|
|
|
|
Cumulative DPU plot |
|
|
DPU |
|
This capability study includes enough samples to estimate mean DPU. |
|
|
sample |
|