Exponential distribution
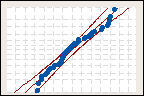
Normal distribution
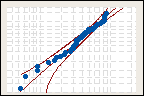
3-parameter Weibull distribution
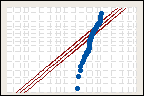
Anderson-Darling statistic = 9.599
p-value < 0.003
Anderson-Darling statistic = 0.641
p-value = 0.089
Anderson-Darling statistic = 0.376
p-value = 0.432
Determine whether a statistical model fits your data by analyzing the difference between your observed values and their expected values in the model. For continuous data, you can assess goodness-of-fit visually with a probability plot, or quantitatively with a hypothesis test such as the Anderson-Darling test. For categorical data, you can use a chi-square test or Minitab's goodness-of-fit test for Poisson data. Minitab also performs goodness-of-fit tests for logistic regression models.
Goodness-of-fit tests use the following hypotheses:
For example, you want to find the distribution that best models the failure times of light bulbs. You run life testing on a sample of light bulbs to observe their failure times. You compare three distributions for the goodness-of-fit they offer your data with Minitab's probability plot.
|
Exponential distribution |
Normal distribution |
3-parameter Weibull distribution |
|
|
|
|
|
Anderson-Darling statistic = 9.599 p-value < 0.003 |
Anderson-Darling statistic = 0.641 p-value = 0.089 |
Anderson-Darling statistic = 0.376 p-value = 0.432 |
The p-value for the exponential distribution is low enough to reject the null hypothesis of a good fit. At an alpha-level of 0.05, both the normal distribution and the 3-parameter Weibull distribution provide a good fit for your data. Some analysts choose the distribution with the highest p-value, but any distribution with a nonsignificant p-value is acceptable.