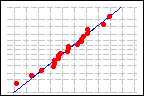
Probability Plot of Normal Data
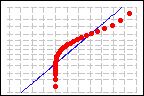
Probability Plot of Nonnormal Data
A one-sample hypothesis test to determine whether the population from which you draw your sample is nonnormal. Many statistical procedures rely on population normality, and using a normality test to determine whether to reject this assumption can be an important step in your analysis. The null hypothesis for a normality test states that the population in normal. The alternative hypothesis states that the population is nonnormal. To determine whether your sample data come from a nonnormal population, you can choose from four tests.
You can assess population normality with a normal probability plot, which plots the ordered data values against values that you expect them to be near if the sample's population is normally distributed. If the population is normal, the plotted points will form an approximately straight line.
|
Probability Plot of Normal Data |
Probability Plot of Nonnormal Data |
|
|
|
|
|
|
This test compares the empirical cumulative distribution function of your sample data with the distribution expected if the data were normal. If this observed difference is sufficiently large, the test will reject the null hypothesis of population normality.
This test assesses normality by calculating the correlation between your data and the normal scores of your data. If the correlation coefficient is near 1, the population is likely to be normal. The Ryan-Joiner statistic assesses the strength of this correlation; if it falls below the appropriate critical value, you will reject the null hypothesis of population normality. This test is similar to the Shapiro-Wilk normality test.
This test compares the empirical cumulative distribution function of your sample data with the distribution expected if the data were normal. If this observed difference is sufficiently large, the test will reject the null hypothesis of population normality.
If the p-value of these test is less than your chosen a-level, you can reject your null hypothesis and conclude that the population is nonnormal.
An informal approximation of a normality test, called "the fat pencil test", is often applied to a probability plot. Imagine a "fat pencil" lying on top of the fitted line: if it covers all the data points on the plot, the data is probably normal; if points are far enough from the fitted line that they are visible beyond the edges of the fat pencil, the data is probably nonnormal. This informal method is not a substitute for the statistical inference of the normality test itself, but it is useful as a quick visual assessment. In the graphs below, the fat pencil test is applied to the probability plots above. The grey bands represent a fat pencil laying on top of the fitted line.
|
The "Fat Pencil Test" with normal data |
The "Fat Pencil Test" with nonnormal data |
|
|
|