Probability plot

Use to evaluate the fit of a distribution to your data, estimate percentiles, and compare different sample distributions. A probability plot does the following:

· Plots each value vs. the percentage of values in the sample that are less than or equal to it, along a fitted distribution line (middle line).

The scales are transformed as necessary so that the fitted distribution forms a straight line.

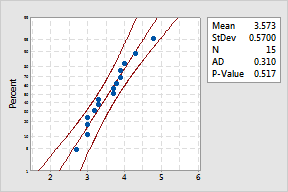
· May display the approximate 95% confidence intervals (curved lines) for the percentiles.

· May display a table with distribution parameter estimates along with the Anderson-Darling statistic and P-value to help you evaluate the distribution fit to your data.

For example, a regional fast food restaurant manager would like to know the percentage of customers who have to wait the target time of 4 minutes or less for their food. He records the wait times for 15 customers, represented by the probability plot above. The probability plot reveals the following:

· Because the data points roughly follow the straight line, the p-value is over 0.05, and the AD statistic is low, he can conclude that the data are from a normally distributed population. Therefore, he can use the fitted line to estimate percentiles. If it hadn't fit, he could try fitting other distributions.

· The mean wait time is 3.573; the standard deviation is 0.5700.

· It appears that about 80% of the data fall below 4.0. He can hover the cursor over one of the lines to get exact numbers, or add a percentile line at 4 minutes.

The plot above shows samples from only one restaurant. The manager could also display and compare data for several restaurants on the same probability plot.

A probability plot performs a similar function as an empirical CDF plot. An advantage of a probability plot is that you can judge the distribution fit by viewing how the points fall about the line.

Probability plots are also known as Rankit, QQ, Quatile, and PP plots.