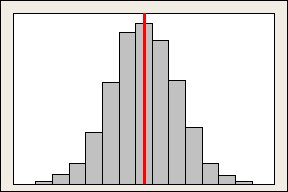
Symmetrical or non-skewed distributions

As data becomes more symmetrical, its skewness value approaches zero. Normally distributed data, by definition, exhibits relatively little skewness. By drawing a line down the middle of this histogram of normal data it's easy to see that the two sides mirror one another.

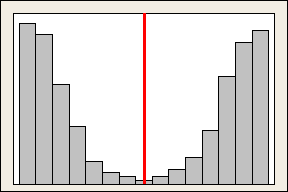
But lack of skewness alone doesn't imply normality. The two sides of this distribution still mirror one another, though the data is far from normally distributed.

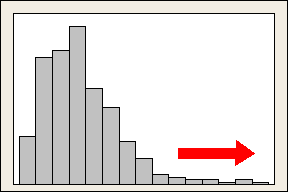
Positive or Right skewed distributions

Positive skewed or right skewed data is so named because the "tail" of the distribution points to the right, and because its skewness value will be greater than 0 (or positive). Salary data is often skewed in this manner: many employees in a company make relatively little, while increasingly few people make very high salaries.

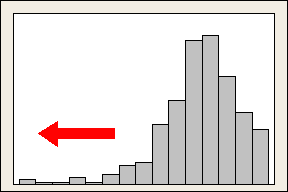
Negative or Left skewed distributions

Here's an example of left skewed or negative skewed data (the distribution's tail points to the left, and it produces a negative skewness value). Failure rate data is often left skewed. Consider light bulbs: very few will burn out right away, the vast majority lasting for quite a long time.