Variance

A measure of dispersion, which is the extent to which a data set or distribution is scattered around its mean.

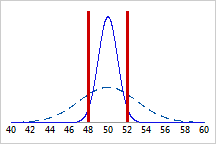
Monitoring variance is essential to the manufacturing and quality industries because a reduction of process variance increases precision and reduces the number of defects. For example, a factory produces carpentry nails that are 50mm in length, and a nail meets specifications if its length is within 2mm of the target value of 50mm. The factory uses two types of machines to manufacture nails. Both machines produce nails with normally distributed lengths and a mean length of 50mm. However, nails from each machine have different variances: Machine A, with the dotted-line distribution below, produces nails with a variance of 9mm2, and Machine B, with the solid-line distribution below, produces nails with a variance of 1mm2. The distributions of nail length for each machine are superimposed, along with the vertical upper and lower specification bounds:

Nail length from Machine A has a larger variance than nail length from Machine B. Therefore, any given nail from Machine A has a greater chance of being outside the specification limits than a nail from Machine B.

Because variance (s2) is a squared quantity, its units are also squared and may be confusing to discuss in practice. For example, a sample of waiting times at a bus stop may have a mean of 15 minutes and a variance of 9 minutes2. To resolve this confusion, variance is often displayed with its square root, the standard deviation (s), which is a more intuitive measurement. A variance of 9 minutes2 is equivalent to a standard deviation of 3 minutes.