多重经验累积分布函数图示例
主题     解释结果     会话命令     另请参见 

您想要评估为降低布料易燃性而设计的两种涂层的效力。随机选择了 15 个样本，每种布料都包含没有涂层、应用涂层 A 和应用涂层 B 的布料。检验员随后将每个样本放在明火上固定的一段时间，然后测量燃尽部分的长度。

通常，使用第 87 个百分位数作为此类检验的基准。创建一个经验累积分布函数图来比较每种布料的拟合分布，并估计每个总体的第 87 个百分位数。

1    打开工作表“阻燃材料.MTW”。

2    选择图形 > 经验累积分布函数。

3    选择多个，然后单击确定。

4    在图形变量中，输入布料 - 涂层 B。

5    单击尺度，然后单击百分位数线选项卡。

6    在百分位数线下，选择在 Y 值，并输入 87。单击确定。

7    在每个对话框中单击确定。

图形窗口输出

解释结果

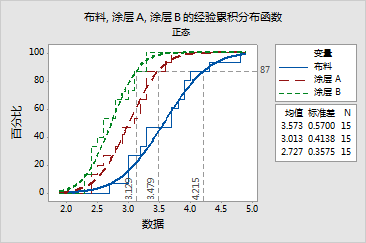
步阶经验累积分布函数与拟合线非常贴近，表明正态分布与这些数据拟合得很好。每个总体的第 87 个估计百分位数为：

·    4.215（对于没有涂层的布料）

·    3.479（对于具有涂层 A 的布料）

·    3.129（对于具有涂层 B 的布料）

变量在输出表中的顺序与在图例中的顺序相同。

涂层 A 似乎减少了布料燃烧，拟合线中的向左偏移和较短的平均燃尽长度（3.013 相较于没有涂层的布料的 3.573）这两点就是证据。此外，涂层 A 似乎还降低了燃尽长度的变异性，其拟合线的斜率较陡和标准差较小（0.4138 相较于 0.5700）这两点就是证据。但是，需要执行适当的检验来确认这些观测值。

涂层 B 可能比涂层 A 更有效。涂层 B 将平均燃尽长度减小到 2.727，并将标准差减小到 0.3575（请参见参数估计）。