Example of an empirical cdf graph
main topics     interpreting results     session command     see also 

You work for a textile manufacturer and want to assess the flammability of a new fabric. Testers hold randomly selected pieces of the fabric over an open flame for a fixed amount of time and measure the length of the burned portion.

You typically use the 87th percentile as a benchmark for such tests. Create an empirical cdf graph to determine if a normal distribution fits your data and to estimate the 87th percentile for the population.

1    Open the worksheet FLAMERTD.MTW.

2    Choose Graph > Empirical CDF.

3    Choose Single, then click OK.

4    In Graph variables, enter Fabric.

5    Click Scale, then click the Percentile Lines tab.

6    Under Percentile Lines, choose At Y values, and enter 87. Click OK in each dialog box.

Graph window output

Interpreting the results

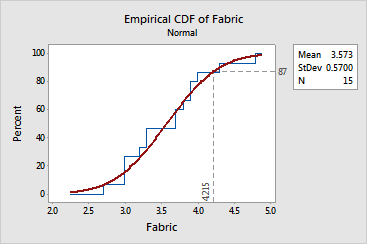
A normal distribution with a mean of 3.573 and a standard deviation of 0.57 (see parameter estimates) appears to fit your sample data fairly well. Because the distribution fits your data, you can use the fitted line to estimate percentiles for the population. The estimated 87th percentile for burn length is 4.215.

You may want to further evaluate the estimate by creating a probability plot, which includes:

·    An Anderson-Darling statistic and p-value to help you verify whether the normal distribution fits your data

·    Confidence intervals for estimated percentiles