Example of a 2-Sample Equivalence Test
main topic     interpreting results     session command     see also 

You created a new, less expensive  formulation of your popular cat food for discount retailers. You want to ensure that the protein content of the discount food is the same as that of your original food. You measure the amount of protein per 100 grams of food in both formulations and test whether they are equivalent within +/- 0.5 grams. You are not confident that the variances are equal, so you do not check Assume equal Variances in the Options subdialog box.

1    Open the worksheet CATFOOD.MTW.

2    Choose Stat > Equivalence Tests > 2-Sample.

3    Choose Samples in different columns.

4    In Test sample, enter Discount.

5    In Reference sample, enter Original.

6    From Hypothesis about, choose Test mean - reference mean.

7    From What do you want to determine, choose Lower limit < test mean - reference mean < upper limit.

8    In Lower limit, enter -0.5.  In Upper limit, enter 0.5.

9    Click OK.

Session window output

Two-Sample Equivalence Test: Discount, Original

 

 

Method

 

Test mean = mean of Discount

Reference mean = mean of Original

Equal variances were not assumed for the analysis.

 

 

Descriptive Statistics

 

Variable   N    Mean    StDev   SE Mean

Discount  10  33.971  0.58064   0.18361

Original   9  34.092  0.26138  0.087127

 

 

Difference: Mean(Discount) - Mean(Original)

 

Difference       SE         95% CI        Equivalence Interval

  -0.12122  0.20324  (-0.48345, 0.24101)       (-0.5, 0.5)

 

CI is within the equivalence interval. Can claim equivalence.

 

 

Test

 

Null hypothesis:         Difference ≤ -0.5 or Difference ≥ 0.5

Alternative hypothesis:  -0.5 < Difference < 0.5

α level:                 0.05

 

Null Hypothesis    DF  T-Value  P-Value

Difference ≤ -0.5  12   1.8637    0.044

Difference ≥ 0.5   12  -3.0566    0.005

 

The greater of the two P-Values is 0.044. Can claim equivalence.

Graph window output

Interpreting the results

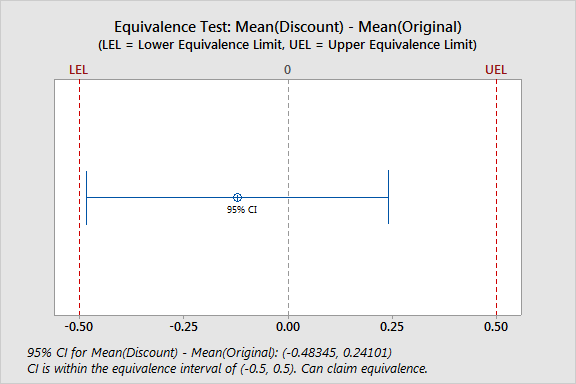
For the cat food data, the confidence interval for the difference is completely within the equivalence interval. Thus you can conclude that the two formulations of cat food contain equivalent amounts of protein.