主题 解释结果 会话命令 另请参见
您记录了 14 个人口普查区的以下特征:总人口(人口)、平均受教育年数(学校)、总就业人数(服务处所)、医疗服务从业人数(健康) 以及住宅均值(家庭)。该数据来自 [6],表 8.2。
通过进行主成份分析了解基础数据结构。由于测量值不是使用相同尺度测量的,因此须使用相关矩阵将测量值标准化。
1 打开工作表“多元分析示例.MTW”。
2 选择统计 > 多变量 > 主成份。
3 在变量中,输入人口-住宅。
4 在矩阵类型下,选择相关。
5 单击图形并选中碎石图和异常值图。
6 在每个对话框中单击确定。
会话窗口输出
主成份分析: 人口, 学校, 服务处所, 健康, 家庭
相关矩阵的特征分析
特征值 3.0289 1.2911 0.5725 0.0954 0.0121 比率 0.606 0.258 0.114 0.019 0.002 累积 0.606 0.864 0.978 0.998 1.000
变量 PC1 PC2 PC3 PC4 PC5 人口 0.558 0.131 -0.008 -0.551 0.606 学校 0.313 0.629 0.549 0.453 -0.007 服务处所 0.568 0.004 -0.117 -0.268 -0.769 健康 0.487 -0.310 -0.455 0.648 0.201 家庭 -0.174 0.701 -0.691 -0.015 -0.014 |
图形窗口输出
第一个主成份的方差(特征值)为 3.0289,占总方差的 60.6%。PC1 下所列系数显示如何计算主成份分值:
PC1 = 0.558 人口 + 0.313 教育 + 0.568 就业 + 0.487 医疗 - 0.174 住宅
应注意到,对主成份的解释是主观的,但常常会表现出明显的模式。例如,可以认为第一个主成份表示整个总体大小、受教育水平、就业水平和医疗服务就业效应,因为这些项的系数具有相同的符号,并且不接近于零。
第二个主成份的方差为 1.2911,占数据变异性的 25.8%。它是使用 PC2 下列出的系数根据原始数据计算得到的。一定程度上,可将此成份视为受教育程度和住宅价值与医疗就业的对比水平。
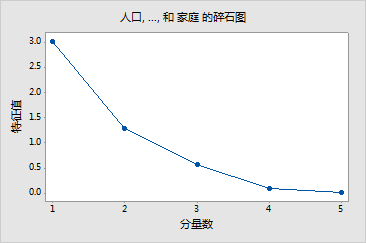
前两个主成份合在一起以及前三个主成份合在一起分别占到了总变异性的 86.4% 和 97.8%。因此,从两到三个基础维度就可以掌握数据结构的大部分情况。其余主成份在变异中所占的比例很小,可能并不重要。碎石图直观地提供了此信息。
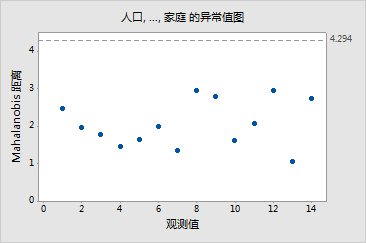
选中异常值非常重要,因为它们会对结果产生显著影响。异常值图会显示工作表中每个观测值的 Mahalanobis 距离。位于 y 轴参考线上方的点就是异常值。人口普查数据中并未显示任何异常值。