二进制拟合线图示例
主题     解释结果     会话命令    另请参见 

一家精神病康复中心记录了每位病人的以下这些数据：

·   收治月份

·   住院时间

·   出院原因：

1: 正常原因

2: 其他原因；例如，不顾医院忠告、法院命令、未请假而擅自离开等

出院原因属于二进制数据，因为这些值要么是正常，要么是其他。因此，二进制 Logistic 回归分析适用于调查住院时间是否影响病人出院的原因。

1    打开工作表“康复中心.MTW”。

2    选择统计 > 回归 > 二元拟合线图。

3    在响应中，输入原因。

4    在预测变量中，输入住院时间。

5    单击选项。

6    在优势比增量中，输入 7。

7    单击确定。

8    单击图形。

9    选择三合一。

10 在每个对话框中单击确定。

会话窗口输出

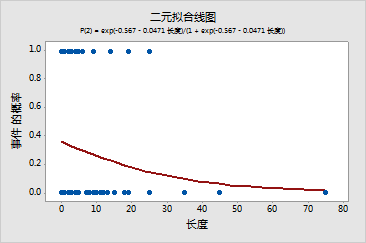
二元拟合线: 原因 与 长度

 

 

* 警告 * 在数据以响应/频率格式显示时，残差与拟合图不可用。

 

二元拟合线图

 

 

 

方法

 

链接函数      Logit

已使用的行数  58

 

 

响应信息

 

变量  值    计数

原因  2       16  （事件）

      1       42

      合计    58

 

 

偏差表

 

                            调整后

来源    自由度  调整后偏差    均值  卡方   P 值

回归         1       2.333   2.333  2.33  0.127

  长度       1       2.333   2.333  2.33  0.127

误差        56      65.991   1.178

合计        57      68.324

 

 

模型汇总

 

           偏差 R-Sq

偏差 R-Sq     (调整)    AIC

    3.41%      1.95%  69.99

 

 

系数

 

                           方差膨

项       系数  系数标准误  胀因子

常量   -0.567       0.396

长度  -0.0471      0.0366    1.00

 

 

连续预测变量的优势比

 

      变更

      单位  优势比    95% 置信区间

长度     7  0.7189  (0.4350, 1.1881)

 

 

回归方程

 

P(2) = exp(-0.567 - 0.0471 长度)/(1 + exp(-0.567 - 0.0471 长度))

 

 

异常观测值的拟合和诊断

 

        观测到

观测值  的概率  拟合值     残差  标准残差

    32  0.0000  0.0637  -0.3627     -0.39     X

    58  1.0000  0.1486   1.9526      2.02  R

 

R  残差大

X  异常 X

 

 

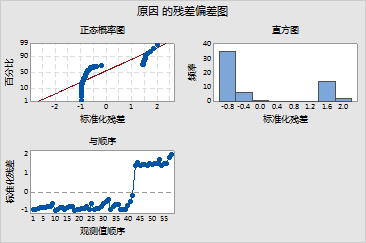
原因 的残差偏差图

图形窗口输出

解释结果

会话窗口输出中包含这些部分：

方法：显示链接函数。在此输出中，您可以看到此模型使用 Logit 链接函数。

响应信息：显示事件数、非事件数和总计。在输出中，您可以看到这些数据包含 42 个正常出院和 16 个其他原因出院的情况。

偏差表：显示这些系数的似然比检验 p 值。在输出中，您可以看到住院时间的估计系数具有大于 0.05 的 p 值。在 a水平为 0.05 时，此证据不足以表明此系数不为零。

模型汇总：显示偏差 R2、调整偏差 R2和 Akaike 信息准则 (AIC)。使用这些统计信息比较不同的模型：

·   偏差 R2为 3.41%。具有相同数量的预测变量的模型中的值越高，表示其他模型的状态越好。由于在增加预测变量时偏差 R2会增大，请使用调整的偏差 R2来比较具有不同预测变量的模型。

·   调整的偏差 R2 为 1.95%。模型中的值越高，表示备择模型的状态越好。调整可确保其他项足以让此模型证明包含这些项。

·   The low values of 偏差 R2和调整的偏差 R2 的较低值表示住院时间并不能很好的解释来说明为什么医院让病人出院。

·   AIC 为 69.99。模型中的值越低，表示备择模型的状态越好。

系数：显示估计系数、系数的标准误和方差膨胀因子 (VIF)。住院时间的估计系数为 -0.0471，表示在住院时间按天变化时 P（因为其他原因医院让病人出院）/P（因为正常原因医院让病人出院）对数的变化。

连续预测变量的优势比： 显示变化单位、优势比和优势比的置信区间。在此分析中，住院时间的单位变化为 7 天。时间的优势比估计为 0.7189，置信区间为 0.4350–1.1881。此优势比的通常解释是，如果住院时间按一周增加，则因为其他原因医院让病人出院的优势将降低 0.7189 倍。

异常观测值的拟合和诊断：显示有关观测值的统计量以及大于 2 的标准化残差或较大的杠杆率值。统计信息包括观测概率、预测概率、残差和标准化残差。观测值 32 属于异常值，因为住院时间 45 太长，并且仍对回归有足够的权重，应值得注意。观测值 58 属于异常值，因为病人因其他原因出院，即使此模型预测医院会因为正常原因（病人住院 25 天）让此病人出院也是如此。

图：在此示例中，您选择了三个诊断图。虽然您可以看到观测值 58 具有最大残差，但这些图不会显示与剩余数据偏离的任何点。由于因其他原因出院比较少见，因此，此模型会预测因正常原因医院让病人出院的概率更高。与因正常原因医院让病人出院相比，在因其他原因医院让病人出院时，其残差与零的差距更大。

这些残差不服从正态分布。因此，二进制拟合线图上的置信区间不可靠。

二进制拟合线图显示住院时间和出院原因之间的关系比较弱。