主题 解释结果 会话命令 另请参见
您正在研究特定机器设置与所消耗能量之间的关系。已知此关系具有相当大的弯曲,而您认为对响应变量进行对数变换将生成更对称的误差分布。您选择使用二次模型为机器设置和所消耗能量之间的关系建模。
1 打开工作表“回归示例.MTW”。
2 选择统计 > 回归 > 拟合线图。
3 在响应 (Y) 中,输入能量消耗。
4 在预测变量 (X) 中,输入机器设置。
5 在回归模型类型中,选择二次。
6 单击选项。在变换下,选中 Y 的常用对数和显示 Y 变量的对数尺度。在显示选项下,选中显示置信区间和显示预测区间。在每个对话框中单击确定。
会话窗口输出
多项式回归分析:能量消耗 与 机器设置
回归方程为 log10(能量消耗) = 7.070 - 0.6986 机器设置 + 0.01740 机器设置^2
S = 0.167696 R-Sq = 93.1% R-Sq(调整) = 91.1%
方差分析
来源 自由度 SS MS F P 回归 2 2.65326 1.32663 47.17 0.000 误差 7 0.19685 0.02812 合计 9 2.85012
方差的序贯分析
来源 自由度 SS F P 线性 1 0.03688 0.10 0.754 二次 1 2.61638 93.04 0.000
拟合线:能量消耗 与 机器设置 |
图形窗口输出
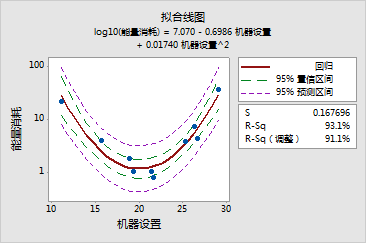
二次模型(p 值 = 0.000,或实际 p 值 < 0.0005)看上去良好地拟合了数据。R![]() 表明机器设置占所消耗能量取 log10 的变异量的 93.1%。通过检查此图,可以发现数据随机地散布在回归线周围,表明不存在系统失拟。还会显示所消耗能量的 log10 的 95% 置信限 (95% CI) 和新观测值的 95% 预测限 (95% PI)。
表明机器设置占所消耗能量取 log10 的变异量的 93.1%。通过检查此图,可以发现数据随机地散布在回归线周围,表明不存在系统失拟。还会显示所消耗能量的 log10 的 95% 置信限 (95% CI) 和新观测值的 95% 预测限 (95% PI)。