主题 解释结果 会话命令 另请参见
美国国家标准与技术研究院 (NIST) 的研究人员希望了解半导体的电子移动性与密度的自然对数之间的关系。此数据可从 NIST 公开获取 (Thurber, R., 1979)。先前研究表明,具有 7 个参数的非线性有理模型(2 个多项式之比)提供了充分拟合。可以通过 [4] 中讨论的方法得到初始值。
1 打开工作表“移动性.MTW”。
2 选择统计 > 回归 > 非线性回归。
3 在响应中,输入移动性。
4 在预期函数中的直接编辑下,输入 (b1+b2*'密度 Ln'+b3*'密度 Ln'**2+b4*'密度 Ln'**3)/ (1+b5*'密度 Ln'+b6*'密度 Ln'**2+b7*'密度 Ln'**3)。
5 单击参数。
6 在必需的初始值下,按照从 b1 到 b7 的顺序,在每个单元格中输入一个值:1300、1500、500、75、1、0.4、0.05。
7 单击确定。
8 单击图形。
9 在包含数据的拟合曲线图下,选中显示置信区间和显示预测区间。
10 在残差下,选择四合一。
11 单击确定。
12 单击结果。
13 选中显示置信区间。
14 在每个对话框中单击确定。
会话窗口输出
非线性回归: 迁移率 = (b1 + b2 * '密度 Ln' + b3 * '密度 Ln' ** 2 + ...
方法
算法 Gauss-Newton 最大迭代次数 200 公差 0.00001
参数的起始值
参数 值 b1 1300 b2 1500 b3 500 b4 75 b5 1 b6 0.4 b7 0.05
方程
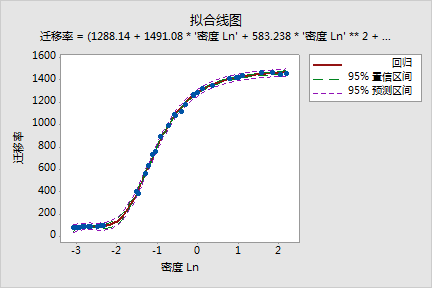
迁移率 = (1288.14 + 1491.08 * '密度 Ln' + 583.238 * '密度 Ln' ** 2 + 75.4167 * '密度 Ln' ** 3) / (1 + 0.966295 * '密度 Ln' + 0.397973 * '密度 Ln' ** 2 + 0.0497273 * '密度 Ln' ** 3)
参数估计
标准误 参数 估计 估计值 95% 置信区间 b1 1288.14 4.6648 (1278.59, 1297.71) b2 1491.08 39.5711 (1381.50, 1548.27) b3 583.24 28.6986 ( 502.36, 625.87) b4 75.42 5.5675 ( 59.58, 83.57) b5 0.97 0.0313 ( 0.88, *) b6 0.40 0.0150 ( 0.36, *) b7 0.05 0.0066 ( 0.03, 0.06)
迁移率 = (b1 + b2 * '密度 Ln' + b3 * '密度 Ln' ** 2 + b4 * '密度 Ln' ** 3) / (1 + b5 * '密度 Ln' + b6 * '密度 Ln' ** 2 + b7 * '密度 Ln' ** 3)
失拟
没有仿行。 Minitab 无法根据纯误差进行失拟检验。
汇总
迭代 27 最终 SSE 5642.71 DFE 30 MSE 188.090 S 13.7146
* 警告 * 某些参数估计值高度相关。考虑简化期望函数或变换预测变量或参数以减少共线性。 |
图形窗口输出
Minitab 利用您指定的预期函数和参数初始值使用 Gauss-Newton 算法进行 27 次迭代后达到了收敛标准。但是,收敛本身并不能保证模型拟合最优或误差平方和 (SSE) 最小。局部 SSE 最小、初始值错误或预期函数不正确都会导致在错误参数值的条件下收敛。因此,至关重要的是,对参数值、拟合线图和残差图进行检查,确保模型充分拟合数据且算法在整体 SSE 最小的条件下收敛。
收敛将得到下面的方程式:
移动性 = (1288.14 + 1491.08 * '密度 Ln' + 583.238 * '密度 Ln' ** 2 + 75.4167 * '密度 Ln' ** 3) /
(1 + 0.966295 * '密度 Ln' + 0.397973 * '密度 Ln' ** 2 + 0.0497273 * '密度 Ln' ** 3)
Minitab 不计算这些参数的 p 值。对于线性回归,每个参数的原假设值为 0(没有效应),而且 p 值以此值为基础。在非线性回归中,每个参数的正确原假设值取决于预期函数以及参数在预期函数中的位置。Minitab 可显示每个参数估计值的置信区间,而不是 p 值。利用学科领域知识和预期函数确定此范围是否合理以及它表示的是否是一个显著效应。
例如,参数 b1 的点估计为 1288.14 且 95% 置信区间为 (1278.61, 1297.67)。研究人员将其视为表示显著性的合理范围。
对于某些数据集、预期函数和置信水平,其中一个或两个置信边界可能不存在。对于移动性数据,参数 b5 和 b6 没有上限。当置信区间缺少边界时,较低的置信水平可能产生双侧区间。在本例中,如果将置信水平降到 92%,Minitab 就会为 b5 和 b6 计算双侧区间。
对于此数据集,Minitab 不会执行失拟检验,因为没有仿行。请检查模型汇总值、拟合线图和残差图以评估拟合情况。
对于非线性回归,Minitab 不会计算整个模型的 R2 或 p 值,因为这些值在线性模型环境外通常没什么意义。因此,当研究人员评估拟合情况并比较竞争的非线性模型时,他们通常会根据学科领域知识、何者的最终 SSE 或 S 值最小以及图形输出进行选择。
S 值解释起来通常更直观一些,无论单就 S 值本身而言还是与竞值进行比较,因为 S 是用与响应变量(电子移动性)相同的单位表示的。在本例中,S 为 13.7146,表示观测到的电子移动性值与拟合移动性值的标准距离(粗略平均绝对距离)为 13.7146 个单位。
关于高度相关参数的警告表明,至少有一对参数相关性的绝对值大于 0.99。您可以考虑是否采取该警告的建议。
带原始数据的拟合线图似乎表明拟合程度适当。点与线相当接近,紧随曲线分布,没有任何系统性偏离。由于方程太长,因此图形中没有显示完整。要查看完整的方程,您可以对图形进行编辑或查看会话窗口输出。
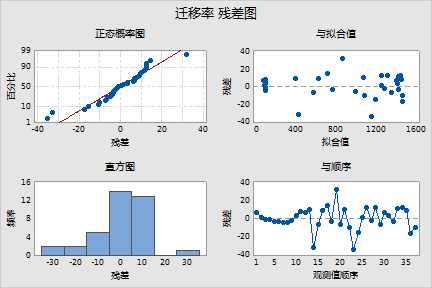
直方图没有显示任何异常值,但它稍微有点偏斜。不过,可使用正态概率图评估正态性。
正态概率图显示一个与正态分布一致的近似线性模式。
残差与拟合值图显示随机模式,表明残差具有恒定方差。有关非恒定方差的信息,请参见 [9]。
残差与顺序图显示数据收集的顺序,可以用来发现非随机误差,特别是与时间相关的效应。残差与顺序图显示前 13 个数据点的非随机模式。应对这些点进行分析研究,确定为什么存在这种模式,并确定测量系统或数据收集过程是否有不当之处。