主题 解释结果 会话命令 另请参见
在拟合 ARIMA 模型的示例中,发现具有 12 次季节差分的 AR(1) 模型与食品部门雇佣数据拟合得很好。现在使用此拟合预测接下来 12 个月的雇佣情况。
步骤 1:在不显示残差的 acf 和 pacf 的情况下重新拟合 ARIMA 模型
1 执行 ARIMA 示例中的 1 - 4 步。
步骤 2:显示时间序列图
1 单击图形。选中时间序列图。单击确定。
步骤 3:生成预测
1 单击预测。在预测点数中,输入 12。在每个对话框中单击确定。
会话窗口输出
综合自回归移动平均 (ARIMA) 模型: 食品
每次迭代中的估计值
迭代 SSE 参数 0 95.2343 0.100 0.847 1 77.5568 0.250 0.702 2 64.5317 0.400 0.556 3 56.1578 0.550 0.410 4 52.4345 0.700 0.261 5 52.2226 0.733 0.216 6 52.2100 0.741 0.203 7 52.2092 0.743 0.201 8 52.2092 0.743 0.200 9 52.2092 0.743 0.200
每个估计值的相对变化不到 0.0010
参数的最终估计值
类型 系数 系数标准误 T P AR 1 0.7434 0.1001 7.42 0.000 常量 0.1996 0.1520 1.31 0.196
差值:0 正规,顺序 12 的 1 周期 观测值个数:原始序列 60,48 差值之后 残差:SS = 51.0364(不包括向后预测) MS = 1.1095 DF = 46
修正 Box-Pierce(Ljung-Box)卡方统计量
滞后 (Lag) 12 24 36 48 卡方 11.3 19.1 27.7 * 自由度 10 22 34 * P 值 0.338 0.641 0.768 *
从周期 60 后开始的预测
95% 限制 周期 预测 下限 上限 实际 61 56.4121 54.3472 58.4770 62 55.5981 53.0251 58.1711 63 55.8390 53.0243 58.6537 64 55.4207 52.4809 58.3605 65 55.8328 52.8261 58.8394 66 59.0674 56.0244 62.1104 67 69.0188 65.9559 72.0817 68 74.1827 71.1089 77.2565 69 76.3558 73.2760 79.4357 70 67.2359 64.1527 70.3191 71 61.3210 58.2360 64.4060 72 58.5100 55.4240 61.5960 |
图形窗口输出
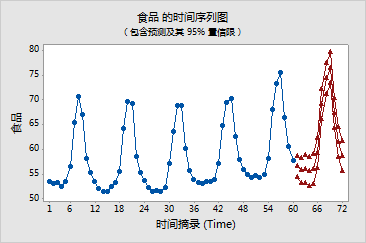
ARIMA 使用 AR(1) 模型在会话窗口和图形窗口中给出置信限为 95% 的预测。季节因素决定未来 12 个月的预测情况,且预测值比前 12 个月稍高。