主题 解释结果 会话命令 另请参见
执行 12 阶差分后,食品雇佣情况数据的 ACF 和 PACF(请参见自相关示例和偏自相关示例)建议使用 1 阶(即 AR(1))自回归模型。在此拟合该模型,检查诊断图并检查拟合优度。要执行 12 阶的差分,请将季节周期指定为 12,并将差分的阶数指定为 1。在接下来的示例中,执行预测。
1 打开工作表“服务处所.MTW”。
2 选择统计 > 时间序列 > 综合自回归移动平均 (ARIMA)。
3 在序列项下,输入食品。
4 选中拟合季节模型。在周期中,输入 12。在非季节下的自回归中输入 1。在季节下的差分中输入 1。
5 单击图形。选中残差的 ACF 和残差的 PACF。
6 在每个对话框中单击确定。
会话窗口输出
综合自回归移动平均 (ARIMA) 模型: 食品
每次迭代中的估计值
迭代 SSE 参数 0 95.2343 0.100 0.847 1 77.5568 0.250 0.702 2 64.5317 0.400 0.556 3 56.1578 0.550 0.410 4 52.4345 0.700 0.261 5 52.2226 0.733 0.216 6 52.2100 0.741 0.203 7 52.2092 0.743 0.201 8 52.2092 0.743 0.200 9 52.2092 0.743 0.200
每个估计值的相对变化不到 0.0010
参数的最终估计值
类型 系数 系数标准误 T P AR 1 0.7434 0.1001 7.42 0.000 常量 0.1996 0.1520 1.31 0.196
差值:0 正规,顺序 12 的 1 周期 观测值个数:原始序列 60,48 差值之后 残差:SS = 51.0364(不包括向后预测) MS = 1.1095 DF = 46
修正 Box-Pierce(Ljung-Box)卡方统计量
滞后 (Lag) 12 24 36 48 卡方 11.3 19.1 27.7 * 自由度 10 22 34 * P 值 0.338 0.641 0.768 * |
图形窗口输出
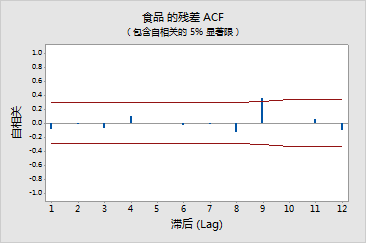
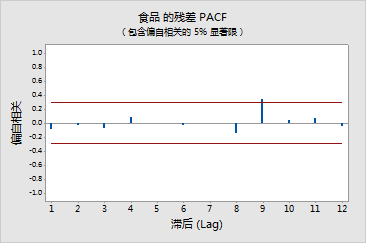
九次迭代后,ARIMA 模型收敛。AR(1) 参数的 t 值为 7.42。作为经验规则,可以认为值大于二时表明相关参数可以认作显著不为零的参数。MSE (1.1095) 可以用于比较各种 ARIMA 模型的拟合度。
Ljung-Box 统计量给出的 p 值不显著,表明残差似乎不相关。残差的 ACF 和 PACF 函数均证明了这一点。假设位于 ACF 和 PACF 函数在滞后 9 的峰值是随机事件的结果。AR(1) 模型似乎拟合得不错,因此可以使用它预测使用 ARIMA 进行预测的示例中的雇佣情况。