主题 解释结果 会话命令 另请参见
假设您为一家生产地面砖的公司工作,并关注砖中出现的扭曲。为确保生产质量,您测量了 10 个工作日中每个工作日生产的 10 块砖的扭曲程度。数据的分布未知。使用“个体分布标识”可以将这些数据与 14 个参数分布和 2 个变换进行拟合。
1 打开工作表“瓦片.MTW”。
2 选择统计 > 质量工具 > 个体分布标识。
3 在数据排列为下,选择单列,然后输入扭曲。
4 选择使用所有分布和变换。单击确定。
会话窗口输出
扭曲 的分布 ID 图
描述性统计量
N N* 均值 标准差 中位数 最小值 最大值 偏度 峰度 100 0 2.92307 1.78597 2.60726 0.28186 8.09064 0.707725 0.135236
Box-Cox 变换: λ = 0.5
Johnson 变换函数: 0.882908 + 0.987049 × Ln( ( X + 0.132606 ) / ( 9.31101 - X ) )
拟合优度检验
极大似 分布 AD P 然比 P 正态 1.028 0.010 Box-Cox 变换 0.301 0.574 对数正态 1.477 <0.005 3 参数对数正态 0.523 * 0.007 指数 5.982 <0.003 2 参数指数 3.660 <0.010 0.000 Weibull 0.248 >0.250 3 参数 Weibull 0.359 0.467 0.225 最小极值 3.410 <0.010 最大极值 0.504 0.213 Gamma 0.489 0.238 3 参数 Gamma 0.479 * 1.000 Logistic 0.879 0.013 对数 Logistic 1.239 <0.005 3 参数对数 Logistic 0.692 * 0.085 Johnson 变换 0.231 0.799
分布参数的极大似然估计
分布 位置 形状 尺度 阈值 正态* 2.92307 1.78597 Box-Cox 变换* 1.62374 0.53798 对数正态* 0.84429 0.74444 3 参数对数正态 1.37877 0.41843 -1.40015 指数 2.92307 2 参数指数 2.66789 0.25518 Weibull 1.69368 3.27812 3 参数 Weibull 1.50491 2.99693 0.20988 最小极值 3.86413 1.99241 最大极值 2.09575 1.41965 Gamma 2.34280 1.24768 3 参数 Gamma 2.38984 1.23136 -0.01968 Logistic 2.79590 1.01616 对数 Logistic 0.90969 0.42168 3 参数对数 Logistic 1.30433 0.26997 -1.09399 Johnson 变换* 0.01120 0.99495
* 尺度:调整后的极大似然估计 |
图形窗口输出
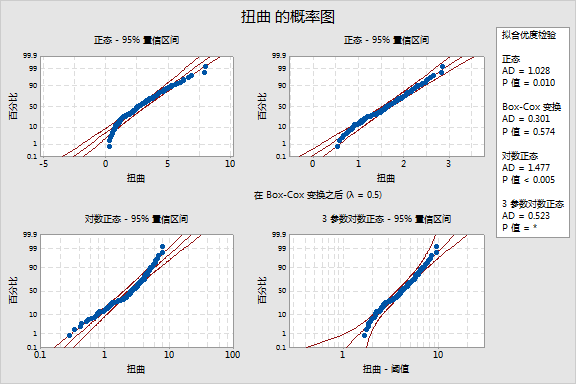
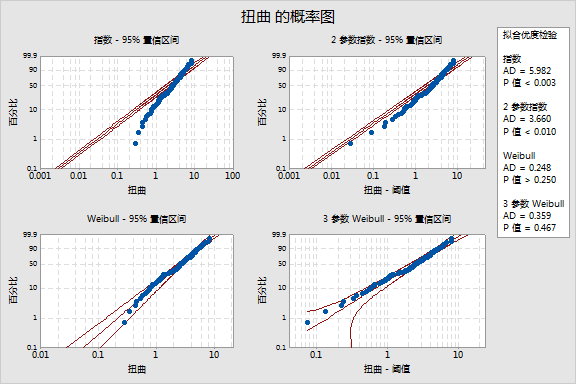
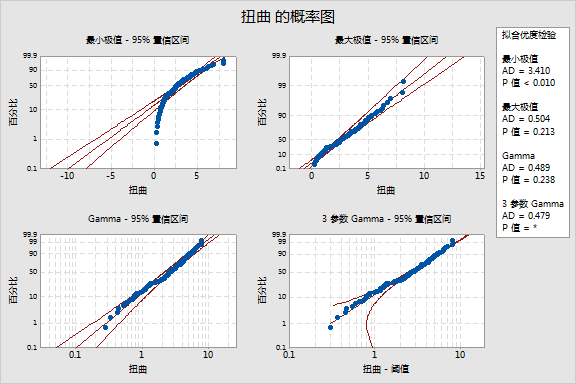
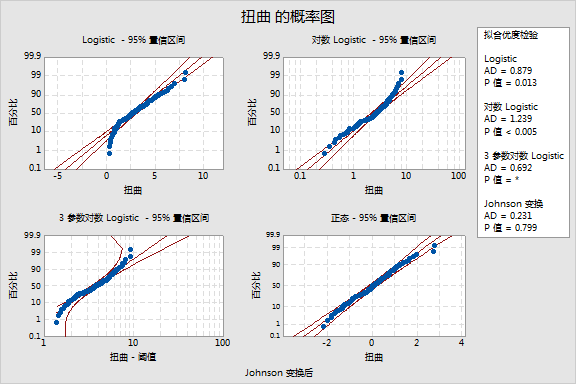
Minitab 显示描述性统计量、拟合优度检验结果和概率图。
描述性统计量 - 描述性统计量表为您提供了整个数据列的摘要信息。所有统计量均基于无缺失 (N = 100) 值。对于这些数据,m = 2.92307,s = 1.78597。
变换 - Box-Cox 变换使用 0.05 的 lambda,而 Johnson 变换函数为 0.882908 + 0.987049 * ln((X + 0.132606) / (9.31101 - X))。
拟合优度检验 - 该表包括 Anderson-Darling (AD) 统计量以及分布的对应 p 值。对于临界值 a,大于 a 的 p 值表明数据服从该分布。Minitab 还包括似然比检验的 p 值 (LRT P),它检验 2 参数分布与数据的拟合程度是否与其 3 参数分布相应项的拟合相当。
大于 0.25、0.467、0.213 和 0.238 的 p 值表明 Weibull、3 参数 Weibull、最大极值和 Gamma 分布与数据的拟合良好。Box-Cox(p 值 = 0.574)和 Johnson 变换(p 值 = 0.799)也较好地拟合了数据。
使用 LRT P 值确定相应的 3 参数分布是否比 2 参数分布的拟合有所改进。LRT P 值 0.225 表明与 2 参数 Weibull 分布相比,3 参数 Weibull 分布并未显著改进拟合。LRT P 值 1.000 表明与 2 参数 Gamma 分布相比,3 参数 Gamma 分布并未显著改进拟合。但是,3 参数对数正态分布比 2 参数对数正态分布有所改进 (LRT P = 0.007),而 2 参数指数分布比指数分布有所改进 (LRT P = 0.000)。
概率图 - 概率图包括有序数据集相应概率的百分位数点。中线是根据以极大似然参数估计为基础的分布得到的预期百分位数。左侧和右侧线代表每个百分位数的置信区间的下限和上限。
概率图显示,对于 2 参数 Weibull、3 参数 Weibull、最大极值和 Gamma 分布,数据点近似成一条直线,并在置信区间内。
如果有多个分布与数据相拟合,请参见选择分布作为指导。如果正态和非正态模型与数据的拟合基本相同,则选择正态模型可能更好,因为它同时估计整体和组内过程能力。有关使用这些数据的其他示例,请参见非正态数据能力分析示例和使用 Box-Cox 变换的能力分析示例。