|
|
Plot Mixture DesignFactorial Plots - Interaction Plot |
Use an interactions plot to visualize the interaction effect of two process variables on the response and to compare the relative strength of the effects. Minitab draws an interactions plot for two process variables, or a matrix of plots for three or more process variables.
For each combination of process variables, Minitab plots the response mean and connects the points for the low and high levels of the process variable plotted on the x-axis. Look at the lines connecting the levels to determine whether or not an interaction is present. You should only view the interaction effects plots for interactions that are significant according to the estimated regression coefficients table. An interaction is present when the change in the response mean from the low to the high level of a factor depends on the level of a second factor.
Remember that plots just indicate patterns. To determine if a pattern is statistically significant, you must do an appropriate test.
Example Output |
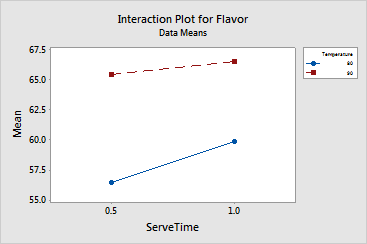
Interpretation |
For the fondue data, the lines on the plot appear to be close to parallel so there is no evidence of an interaction between serving temperature and serving time. That is, the effect of one of these process variables on the response is not influenced by the other process variable.