正态分布(Normal distribution)代表了宇宙中大多数情况的运转状态。大量的随机变量被证明是正态分布的。任何一个分布只要具有以下特征,则可以称为正态分布:
- 分布的平均值、中位数和模式一致。
- 分布曲线是钟形的,关于线 x = μ 对称。
- 曲线下的总面积为1。
- 有一半的值在中心的左边,另一半在右边。
正态分布与二项分布有着很大的不同。然而,如果试验次数接近于无穷大,则它们的形状会变得十分相似。
遵循正态分布的随机变量X的值由下式给出:
正态分布(Normal distribution)
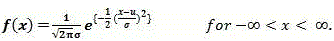
正态分布的随机变量X的均值和方差由下式给出:
均值 -> E(X) = µ
方差 -> Var(X) = σ^2
其中,μ(平均)和σ(标准偏差)是参数。
随机变量X〜N(μ,σ)的图如下所示。
正态分布
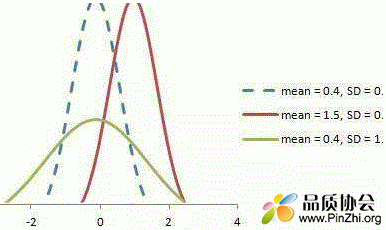
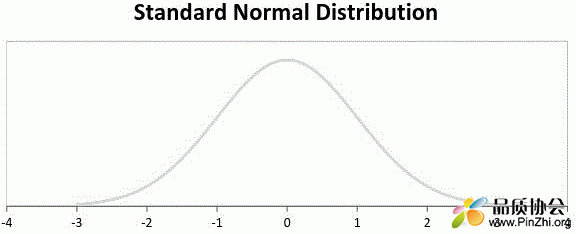
标准正态分布定义为平均值等于0,标准偏差等于1的分布:
标准正态分布

Standard Normal distribution.GIF
泊松分布(Poisson distribution)和二项分布(Binomial distribution)
http://www.pinzhi.org/forum.php?mod=viewthread&tid=60678
正态分布和泊松分布、二项分布的关系及区别
正态分布(Normal distribution)是在满足以下条件的情况下二项分布的另一种限制形式:
1. 试验次数无限大,n → ∞。
2. p和q都不是无限小。
正态分布也是参数λ → ∞的泊松分布的极限情况。
|