Using Process Report to Identify Process Mean Shiftsmain topic
Using Process Report to Identify Process Mean ShiftsSuppose you have a process with a target of 40, a lower specification limit of 38, and an upper specification limit of 42. You collect data in subgroups of size 5 and have found that your process is nearly centered on target (process mean = 40.0016 and ST standard deviation = 0.960).
You add another 20 subgroups of size 5. The mean shifts for the new subgroups to 41.5, which is about a 1.5 sigma shift.
The process reports show:
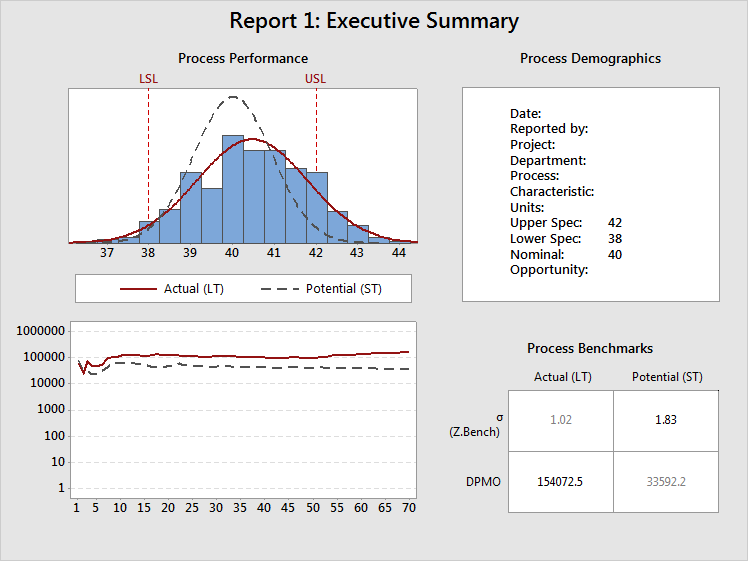
Immediately, you discover a problem by examining the Cumulative DPMO plot. The Cumulative ST DPMO line has flattened. However, the Cumulative LT DPMO line appears to be stabilizing, but then shifts upwards. The LT statistics are not stable, indicating that something has changed in this process. Investigate the process to determine what has changed.
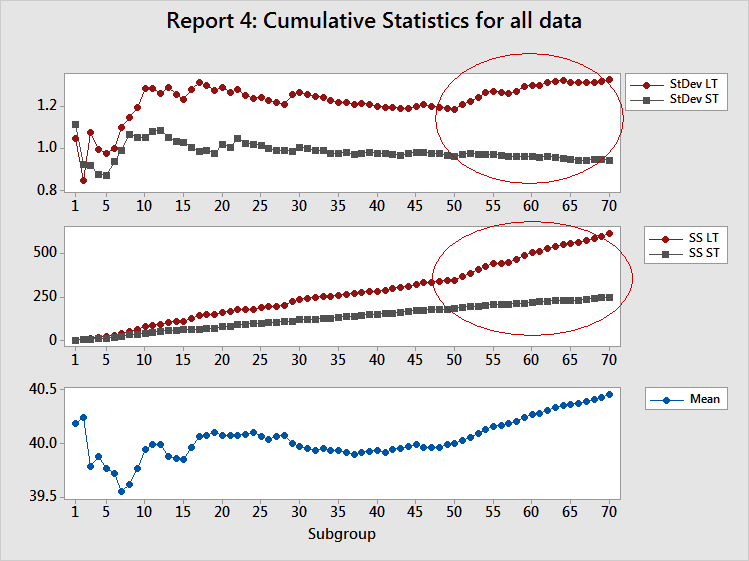
The Cumulative Statistics report reveals:
1 An increase in the LT standard deviation, but none in the ST standard deviation
2 A change in slope for SS LT, but not for SS ST
3 An increase in the cumulative mean
The Cumulative StDev plot displays a marked upturn in slope for the LT standard deviation, with no real change in the ST standard deviation. This change clearly occurs at subgroup 50. When the SS LT slope changes but the SS ST slope does not, a shift in the process mean has occurred. Examine the plot to identify that the change in slope occurs at subgroup 50. The Cumulative Mean plot also indicates a shift in process mean, but it is more difficult to determine where the shift occurred. Thus, the Cumulative SS and Cumulative StDev plots clearly diagnose the problem and show exactly where the problem occurred.
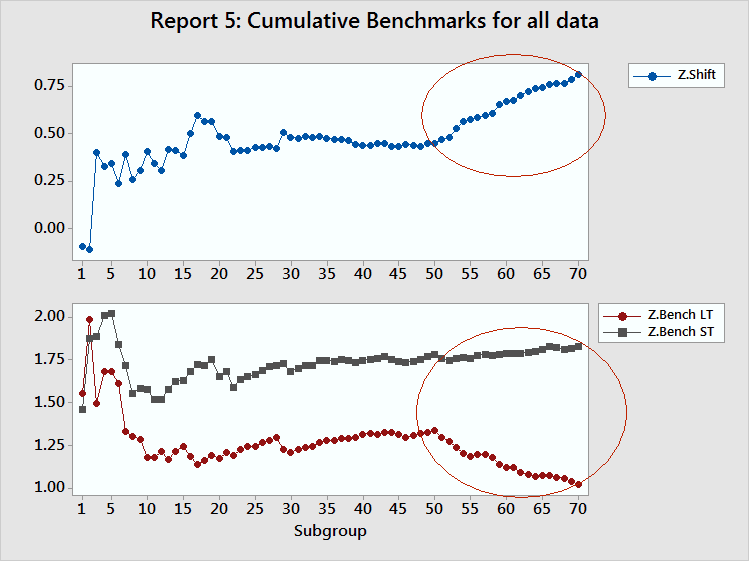
This report displays the effect the shift in process mean has on the Z statistics. The shift in the process mean results in two things:
Moving the mean closer to a specification limit causes both ST and LT capability to drop. Increasing the LT standard deviation, as we saw in Report 4, causes the Z.LT to drop even further. DPMO is calculated directly from the Z.Bench statistics - thus a dramatic change in Z.Bench LT leads to a pronounced upward slope in Cumulative LT DPMO, and a smaller change in Z.Bench ST leads to a slight upward slope in Cumulative ST PPM. See Report 1.
Because Z.Bench LT drops more than Z.Bench ST, we also see an increase in Z.Shift. When you see behavior such as this, do not use the Process Report as is. The report is based on two different processes and you need to determine which process you want to perform the analysis on - the one before or after the change. Once you have made that determination, collect data only from that process and rerun Process Report. If Process Report is used to validate project improvements, do not include data collected before the improvements.