Brake Assembly Example, Part I
main topic     interpreting results     session command     see also   

Suppose you want to establish tolerances for each element in a brake assembly.

You also want to:

·    Compare statistics from your own estimates of tolerances and those calculated using this procedure

·    Limit the width of the gap by entering upper and lower gap specifications

The tolerancing procedure takes place in two steps. The first step uses the Calculate Gap Pools command. The output from this command determines how you do the second part of the procedure using the Allocate Gap Pools command.

1    Open the file BRAKE.MTW. (See data sets.)

2    Choose Six Sigma > Design for Manufacturability > Calculate Gap Pools.

3    In Element names, enter Elements. In Means, enter Means.

4    In Directional vectors, enter 'Dir Vectors'. In Standard deviations, enter 'St Dev'.

5    Under Gap Specification: In Lower spec, type 0.001. In Upper spec, type 0.251.

6    Click Options.

7    In Complexity, enter Cmplx.

8    In Lower spec, enter Lowers. In Upper spec, enter Uppers.

9    Click OK in each dialog box.

Session window output

Tolerance Analysis: Calculate Gap Pools

 

 

Gap Specifications

Before Allocation of Gap Pools

 

Nominal Value         0.126

Lower Spec            0.001

Upper Spec            0.251

 

Required Z.Bench(LT)   4.50

Long-Term Shift        1.50

 

 

Gap Short-Term and Long-Term Statistics

Before Allocation of Gap Pools

 

         Short-Term  Long-Term

Mean       0.126000   0.126000

StDev         0.018      0.032

 

Z.LSL          7.09       3.94

Z.USL          7.09       3.94

Z.Bench        6.99       3.77

 

 

Gap Pool Statistics

 

Mean Pool       0.0000000

Variance Pool  -0.0002839

 

 

Overall Design Statistics

Before Allocation of Gap Pools

 

Rolled Yield     46.91

DPU           0.756952

Z.Bench           1.45

 

 

Gap Distribution Before Allocation

 

 

 

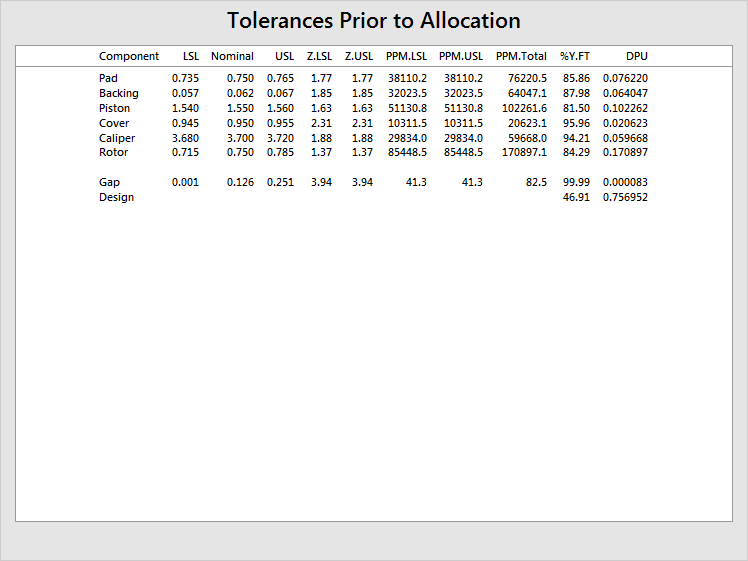
Tolerances Prior to Allocation

Graph window output

Interpreting the results

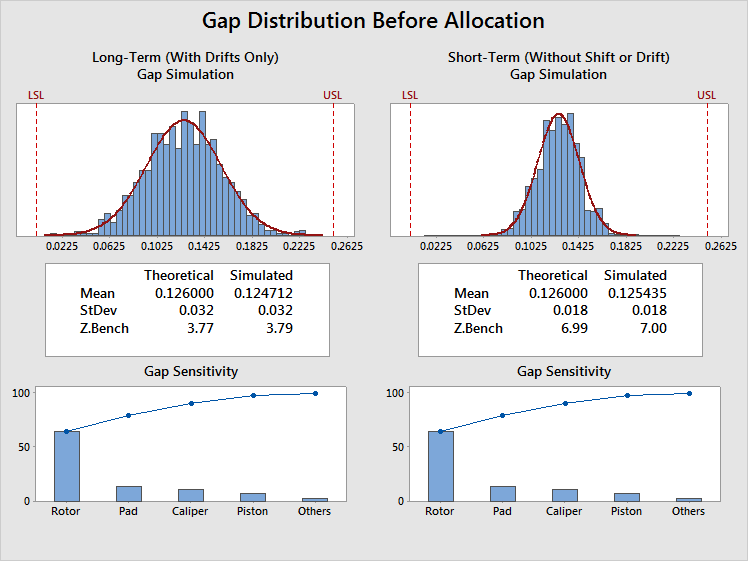
The long-term Gap Z.Bench is 3.77. However, a value of 4.5 is required in order to achieve the desired long-term PPM on the assembly Gap.

The Gap Pool Statistics table shows the gap mean and variance pools. There is no mean pool to allocate, because in this case the short-term gap mean is equal to the midpoint between the gap specification limits. When this happens, the mean pool is always equal to 0. The variance pool is -0.0002839, which means that the long-term gap variance must be reduced by 0.0002839. To accomplish this, we must perform the second stage of the analysis, the allocation stage.

See Calculating the specification limits for more information on calculations.

Click here to continue.