Brake Assembly Example, Part II
main topic     interpreting results     session command     see also  

The second part of the tolerancing procedure uses the Allocate Gap Pools dialog box. Minitab knows that both the gap mean and variance pools were calculated in stage 1. Thus you need to specify two sets of weights-one for each pool.

In this example, the gap mean pool is 0, so it doesn't matter how you allocate it. You decide to make up the gap mean pool 50% by reducing the mean in the pad, 30% by reducing the mean in the backing, and 20% by reducing the mean in the cover.

The gap variance pool is 0.0002839 and you decide to make it up like this:

·    20% by reducing the variance in the piston size

·    30% by reducing the variance in the caliper size

·    50% by reducing the variance in the rotor size

1    If you haven't already, perform steps 1-9 in Brake Assembly Example, Part I.

2    Enter allocation weights in the Data window. For ease, those weights have already been entered in the BRAKE.MTW worksheet for you.

3    Choose Six Sigma > Design for Manufacturability > Allocate Gap Pools.

4    In Allocation weights for Gap variance pool, enter 'Var Alloc'.

5    Click OK.

Session window output

Tolerance Analysis: Allocate Gap Pools

 

 

Gap Specifications

After Allocation of Gap Pools

 

Nominal Value         0.126

Lower Spec            0.001

Upper Spec            0.251

 

Required Z.Bench(LT)   4.50

Long-Term Shift        1.50

 

 

Gap Short-Term and Long-Term Statistics

Before Allocation of Gap Pools

 

         Short-Term  Long-Term

Mean       0.126000   0.126000

StDev         0.018      0.032

 

Z.LSL          7.09       3.94

Z.USL          7.09       3.94

Z.Bench        6.99       3.77

 

 

Gap Pool Statistics

 

Mean Pool       0.0000000

Variance Pool  -0.0002839

 

 

Gap Short-Term and Long-Term Statistics

After Allocation of Gap Pools

 

         Short-Term  Long-Term

Mean       0.126000   0.126000

StDev         0.015      0.027

 

Z.LSL          8.36       4.65

Z.USL          8.36       4.65

Z.Bench           *       4.50

 

 

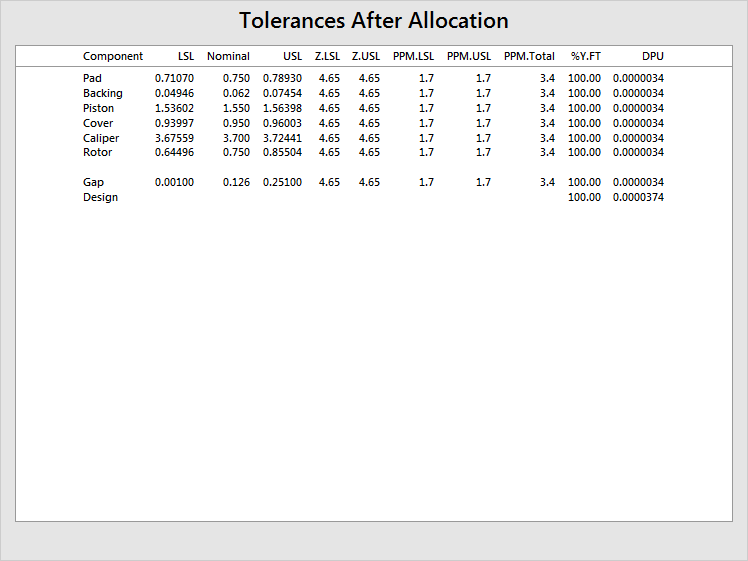
Element Means and Standard Deviations

After Allocation of Gap Pools

 

Pad      0.750  0.0047000

Backing  0.062  0.0015000

Piston   1.550  0.0016723

Cover    0.950  0.0012000

Caliper  3.700  0.0029188

Rotor    0.750  0.0125627

 

 

Overall Design Statistics

After Allocation of Gap Pools

 

Rolled Yield     100.00

DPU           0.0000374

Z.Bench            4.48

 

 

Gap Distribution After Allocation

 

 

 

Tolerances After Allocation

Graph window output

Interpreting the results

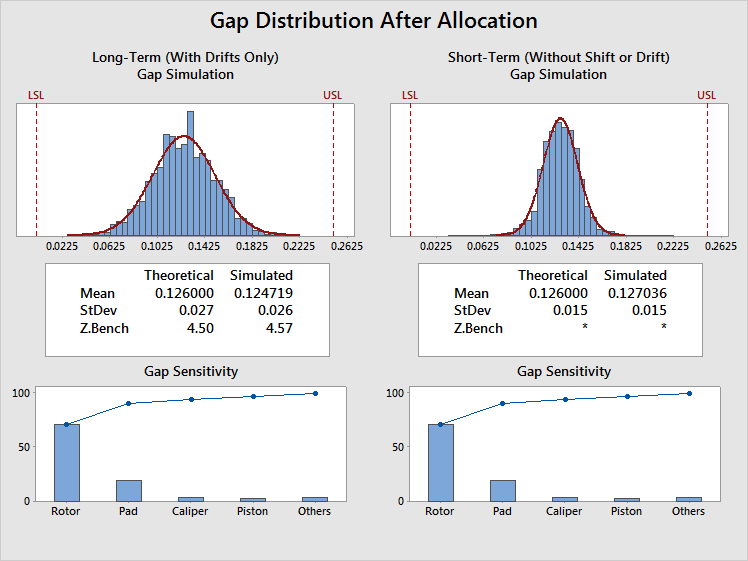
As shown in the Session window output, the long-term gap Z.Bench now equals 4.5, which is the goal. More importantly, the design now has an overall yield of ~100%, compared to the original design's overall yield of 46.91%.

It should be noted that achieving a long-term gap Z.Bench of exactly 4.5 will not always occur with a variance pool, while it should always occur with a mean pool.

The table of adjusted means and standard deviations show what the short-term means and standard deviations must be for each element in the assembly, to achieve the desired long-term performance of the assembly. These values are then used to calculate the optimal tolerances for the elements in the assembly.

See Calculating the specification limits for more information on calculations.