双样本方差检验示例主题 解释结果 会话命令 另请参见
双样本方差检验示例为了提高家庭暖气系统的效率，进行了一项旨在评估两种设备功效的研究。安装其中一种设备后，对房舍的能耗进行了测量。这两种设备分别是电动气闸（气闸 1）和热活化气闸（气闸 2）。您想要确定一种设备的能耗变异性是否高于另一种设备。
能耗数据（气闸内置能量消耗）堆叠在一列中。用一个单独的列（气闸）标识每个行属于哪个样本。
1 打开工作表“炉子.MTW”。
2 选择统计 > 基本统计 > 双方差。
3 选择这两个样本都在一列中。
4 在样本中，输入 '气闸内置能量消耗'。
5 在样本 ID 中，输入气闸。
6 单击确定。
会话窗口输出
双方差检验和置信区间: 气闸内置能量消耗 与 气闸
方法
原假设 σ(1) / σ(2) = 1 备择假设 σ(1) / σ(2) ≠ 1 显著性水平 α = 0.05
统计量
95% 标准差置 气闸 N 标准差 方差 信区间 1 40 3.020 9.120 (2.347, 4.085) 2 50 2.767 7.656 (2.335, 3.413)
标准差比 = 1.091 方差比 = 1.191
95% 置信区间
标准差比置信 方差比置信区 方法 区间 间 Bonett (0.763, 1.494) (0.581, 2.232) Levene (0.697, 1.412) (0.486, 1.992)
检验
检验统 方法 DF1 DF2 计量 P 值 Bonett — — — 0.586 Levene 1 88 0.00 0.996 |
图形窗口输出
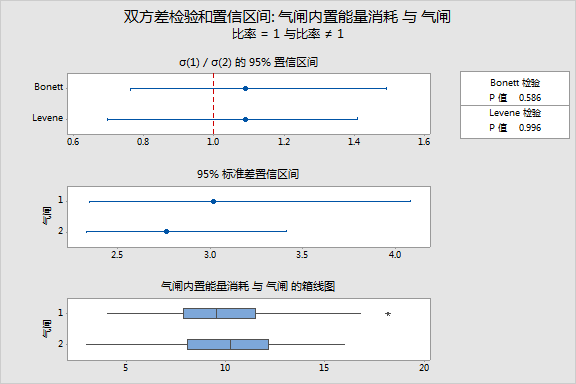
该方法表显示正在检验的假设。因为您接受了默认值，原假设假定两个总体标准差的比率为 1（它们相等），而备择假设假定该比率不为 1（它们不相等）。检验结果显示在输出的底部。
统计表中显示各总体的标准差和方差的样本数量和点估计值。统计表还显示总体标准差或总体方差的置信区间。
Minitab 计算标准差和方差比的 95% 置信区间。如果这些区间包含 1，则没有足够证据表明总体的标准差或方差不相等。
“会话”窗口底部给出 Bonett 检验和 Levene 检验的结果。一般而言，除非有非常偏斜或重尾分布的少量样本，否则应以 Bonett 法作为结论依据。（有关进一步讨论，请参见双方差检验。）
对于能耗示例来说，因为 p 值（0.586 和 0.996）均大于 a 的合理选择范围，因此无法否定标准差相等的原假设。这些数据并未提供足够证据证明两个总体的标准差不相等。