多元回归的示例
主题     解释结果     会话命令    另请参见 

作为太阳能测试的一部分，您测量了各个家庭的总热通量。您希望检查一下总热通量 (HeatFlux) 是否可以通过东、南、北各方向的焦点位置来预测。数据引用自 [33]。您通过使用最佳子集回归发现，最佳双预测变量模型包括了变量“北”和“南”，而最佳三预测变量则增加了变量“东”。您可以使用多元回归来评估三预测变量模型。

1    打开工作表“回归_示例.MTW”。

2    选择统计 > 回归 > 回归 > 拟合回归模型。

3    在响应中，输入热通量。

4    在连续预测变量中，输入东 南 北。

5    单击图形。

6    在残差图下，选择标准化。

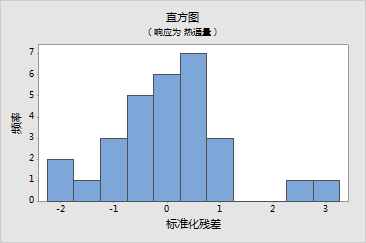
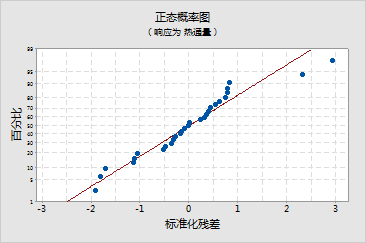
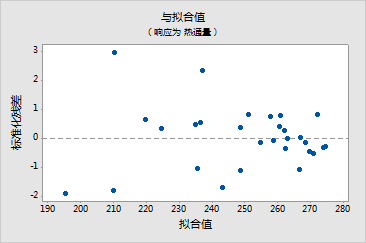
7    在残差图下，选择单独示图。选中残差的直方图、残差的正态概率图以及残差与拟合值。

8    在每个对话框中单击确定。

会话窗口输出

回归分析: 热通量 与 东, 南, 北

 

 

方差分析

 

来源  自由度   Adj SS   Adj MS    F 值   P 值

回归       3  12833.9   4278.0   57.87  0.000

  东       1    226.3    226.3    3.06  0.092

  南       1   2255.1   2255.1   30.51  0.000

  北       1  12330.6  12330.6  166.80  0.000

误差      25   1848.1     73.9

合计      28  14681.9

 

 

模型汇总

 

                 R-sq（调

      S    R-sq      整）  R-sq(预测)

8.59782  87.41%    85.90%      78.96%

 

 

系数

 

              系数标                 方差膨

项      系数    准误    T 值   P 值  胀因子

常量   389.2    66.1    5.89  0.000

东      2.12    1.21    1.75  0.092    1.12

南     5.318   0.963    5.52  0.000    1.21

北    -24.13    1.87  -12.92  0.000    1.09

 

 

回归方程

 

热通量 = 389.2 + 2.12 东 + 5.318 南 - 24.13 北

 

 

异常观测值的拟合和诊断

 

观测值  热通量  拟合值   残差  标准残差

     4  230.70  210.20  20.50      2.94  R

    22  254.50  237.16  17.34      2.32  R

 

R  残差大

解释结果

会话窗口输出

·    方差分析表 (0.000) 中回归模型的 p 值显示，回归过程估计的模型在 0.05 a 水平时是显著的。这表明至少有一个系数不为零。

·    “南”和“北”的估计系数 p 值均为 0.000，表明它们与热通量显著相关。“东”的 p 值为 0.092，表明它在 a 水平为 0.05 时与热通量不相关。此外，序贯平方和表明预测变量“东”无法解释唯一方差的相当一部分。这说明只有变量“北”和“南”的模型可能更合适。  

·    VIF 全部接近 1，说明预测变量不相关。超过 5-10 的 VIF 值说明，由于严重的多重共线性，回归系数的估计效果较差。

·    R2 值表明这些预测变量可以解释“热通量”中 87.41% 的方差。调整 R2 为 85.90%，这说明了模型中预测变量的个数。这两个值都表明模型与数据拟合得很好。

·    预测的 R2 的值为 78.96%。由于预测的 R2 值与 R2  以及调整的 R2 值都很接近，因此模型似乎并没有过度拟合而且具有足够的预测能力。

·    观测值 4 和 22 被标识为异常，因为标准化残差的绝对值大于 2。这表明它们可能是异常值。请参见检查模型、 识别异常值和选择残差类型。

图形窗口输出

·    直方图表明数据中可能存在异常值，因为图的最右端有两个条形。

·    正态概率图显示一个与正态分布一致的近似线性模式。图中右上角的两个点可能是异常值。用笔刷刷图形可将这两个点标识为 4 和 22，同样的点在输出中标记为异常观测值。请参见检查模型和识别异常值。

·    残差与拟合值图显示当拟合值增大时，残差会变小（更接近参考线），这表明这些残差可能具有非恒定方差。有关非恒定方差的信息，请参见 [9]。