主题 解释结果 会话命令 另请参见
在稳定性研究示例中,您利用默认方法确定了一种新药的保质期,该方法将批次作为固定因子处理。如果您从更大的可能批次总体中随机选择批次,那么就可以将批次作为随机因子进行分析。
例如,假定您要计算一种药品的保质期,您随机从一个更大的可能批次总体中选择了 8 个批次的药品。
1 打开工作表“保质期随机.MTW”。
2 选择统计 > 回归 > 稳定性研究 > 稳定性研究。
3 在响应中,输入药物含量。
4 在时间中,输入月。
5 在批次中输入批次。
6 在规格下限中,键入 90。
7 单击选项。
8 选择批次为随机因子。
9 单击确定,然后单击图形。
10 在残差图下,选择四合一。
11 在每个对话框中单击确定。
会话窗口输出
稳定性研究: 药物% 与 月份,批次
因子信息
因子 类型 水平数 水平数 批次 随机 8 1, 2, 3, 4, 5, 6, 7, 8
模型选择,α = 0.25
-2 对 模型 数似然 差值 P 值 月份 批次 月份*批次 128.599 月份 批次 133.424 4.82476 0.059
选定模型中的项: 月份, 批次, 月份*批次
方差分量
来源 变量 总和的 % SE 变量 Z 值 P 值 批次 0.527403 72.91% 0.303847 1.735755 0.041 月份*批次 0.000174 0.02% 0.000142 1.224106 0.110 误差 0.195740 27.06% 0.036752 5.325920 0.000 合计 0.723317
模型汇总
R-sq(调 S R-sq 整) 0.442425 96.91% 96.87%
系数
项 系数 系数标准误 自由度 T 值 P 值 常量 100.060247 0.268705 7.22 372.380078 0.000 月份 -0.138766 0.005794 7.22 -23.950307 0.000
随机效应预测
项 BLUP 标准差 自由度 T 值 P 值 批次 1 1.359433 0.313987 12.45 4.329582 0.001 2 0.395376 0.313987 12.45 1.259213 0.231 3 0.109150 0.313987 12.45 0.347625 0.734 4 -0.409321 0.313987 12.45 -1.303625 0.216 5 -0.135643 0.313987 12.45 -0.432002 0.673 6 -1.064735 0.313987 12.45 -3.391015 0.005 7 0.049419 0.313987 12.45 0.157391 0.877 8 -0.303678 0.313987 12.45 -0.967169 0.352 月份*批次 1 0.006281 0.008581 10.49 0.731927 0.480 2 0.019905 0.008581 10.49 2.319532 0.042 3 -0.013831 0.008581 10.49 -1.611737 0.137 4 0.003468 0.008581 10.49 0.404171 0.694 5 0.001240 0.008581 10.49 0.144454 0.888 6 0.000276 0.008581 10.49 0.032141 0.975 7 -0.010961 0.008581 10.49 -1.277269 0.229 8 -0.006378 0.008581 10.49 -0.743220 0.474
异常观测值的允许值拟合和诊断
观测值 药物% 拟合值 自由度 残差 标准残差 10 101.564000 99.643950 7.04383 1.920050 2.37526 R 31 100.618000 98.811354 7.05287 1.806646 2.21379 R 55 98.481000 96.729866 8.87399 1.751134 2.03349 R
R 残差大
估计稳定期
规格下限 = 90 稳定期 = 您可以 95% 确信至少 95% 的响应高于规格下限的时间期间
所有批次的稳定期 = 53.1819 |
图形窗口输出
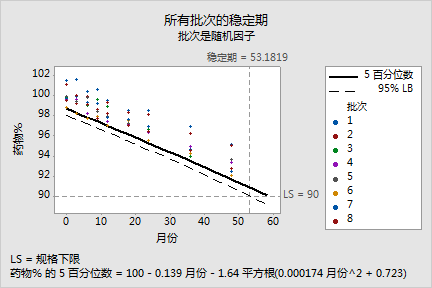
在模型选择过程中,Minitab 将整个模型"月 批次 月和批次"与不含交互作用项的模型对比。由于该比较的 p 值 (0.059) 小于 a (0.25),所以无法从模型中去除交互作用项。最终模型包含月、批次及月和批次交互作用(月*批次)。
当批次因子为随机因子时,Minitab 根据第 95 个百分位数而非第 50 个百分位数计算保质期。(可以在选项子对话框中更改此设置及 a 的值。)在保质期所对应的时间点下,您不再 95% 地确信至少 95% 的响应处于规格限内。 当前数据的保质期约为 53.18 个月。
系数表显示模型中固定效应的估计系数。这些系数是边际拟合方程(如下所示)的截距(常量)和斜率(月),用来预测任何随机批次的拟合值。
药物含量 = 100.06 - 0.13877 月
随机效应预测表显示随机项的预测值。通过这些预测值,可以确定条件拟合方程的截距和斜率,用来预测特定批次的拟合值。(使用 Minitab 的预测功能可以查看这些方程。)例如,批次 1 的截距为 101.359,它等于常量 (100.06) 加上批次 1 (1.359) 的最佳线性无偏预测值 (BLUP)。批次 1 的斜率为 - 0.13248,它等于月 (-0.138766) 加上批次 1 和月份的 BLUP (0.006281)。
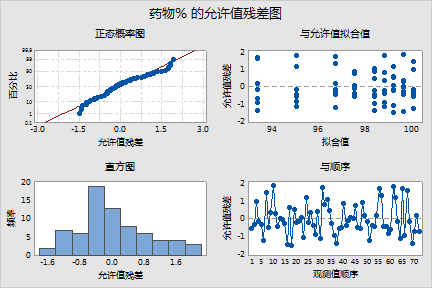
药物含量的边际残差图(上图)显示,在恒定方差下边际残差可能不是正态分布。直方图比正态分布图平坦,并且正态概率图中的点并非完全紧靠线条分布。造成边际残差这种非正态行为的原因之一是当最终模型包含批次和时间交互作用项时,边际残差的方差取决于时间变量,且可能不是恒定的。
可以利用条件残差检查模型中误差项的正态性。
1 按 CTRL+E 或选择统计 > 回归 > 稳定性研究 > 稳定性研究。
2 单击图形。
3 在图中的残差中选择条件常规。
4 在每个对话框中单击确定。
图形窗口输出
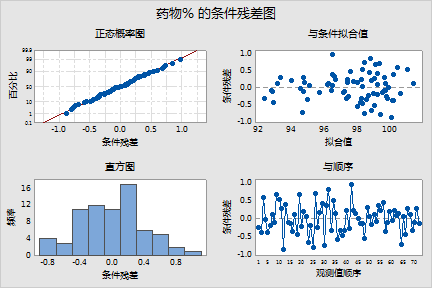
条件残差似乎呈正态分布。整个模型似乎与数据拟合的不错。