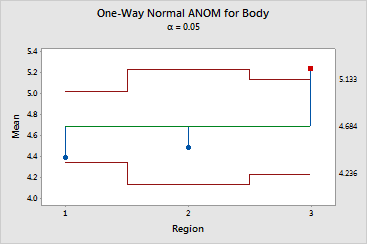
Use the ANOM main effects plot to test the hypothesis that each factor level mean is equal to the overall mean at an a-level you specify. Minitab displays one main effect plot for each factor in a two-way design. The main effects plot shows the following:

·    Plotted points – the sample means at each factor level.

·    Center line (green) – the overall mean.

·    Lower and upper decision limits (red) – used to test the hypothesis. Minitab looks for sample means located beyond the decision limits and marks them with a red symbol.

-    If a sample mean is located beyond a decision limit, you can reject the hypothesis that the mean is equal to the overall mean.

-    If a sample mean falls within the decision limits, you cannot reject the hypothesis that the mean is equal to the overall mean.

Minitab calculates decision limits separately for each level in an ANOM for an unbalanced one-factor design. The limits for a factor level depend on the number of observations at that level.

-    When all levels have the same number of observations, the decision limits are straight lines.

-    When the levels do not all have the same number of observations, then the decision limits change with the level.

Levels that have many observations have decision limits that are closer to the center line than those that have fewer observations.

For the wine data, the graph shows the following:

·    The changing decision limits indicate that the three regions have different numbers of observations. Region 1 has the most observations (17), so its decision limits are the closest to the center line. Region 2 has the fewest observations (10), so its decision limits are the farthest from the center line.

·    The means for both Regions 1 and Region 2 are contained within the decision limits; therefore, the wines from those regions do not differ from the overall mean.

·    The mean for Region 3 is located above the upper decision limit; therefore, the wines from Region 3 are greater than the overall mean.