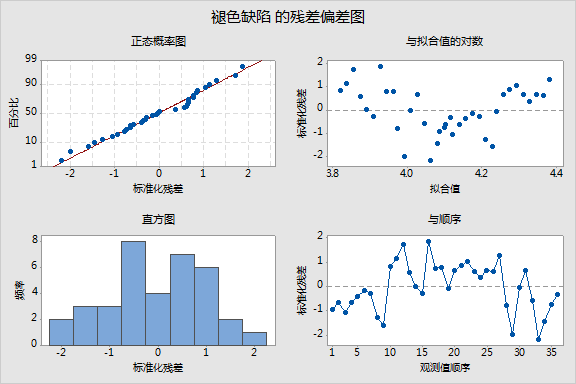
Poisson 回归的示例
主题     解释结果     会话命令    另请参见 

某制造商生产成型树脂零件。软管中的污染和对树脂粒料的磨损可能导致最终产品产生褪色条纹。温度过高和输送速率过快可能导致粒料结块。结块后很难在软管中输送和输送到模具中。该公司每小时采集一次缺陷数数据。

1    打开工作表“树脂缺陷.MTW”。

2    选择统计 > 回归 > Poisson 回归 > 拟合 Poisson 模型。

3    在响应中，输入褪色缺陷。

4    在连续预测变量中，输入清洁小时和温度。

5    在类别预测变量下，输入螺丝钉的大小。

6    单击图形。

7    在残差图下，选择标准化。

8    在残差图下，选择四合一。

9    在每个对话框中单击确定。

会话窗口输出

 

Poisson 回归分析: 褪色缺陷 与 清洁小时, 温度, 螺丝钉的大小

 

 

方法

 

链接函数          自然对数

类别预测变量编码  (1, 0)

已使用的行数      36

 

 

偏差表

 

来源            自由度  调整后偏差  调整后均值   卡方   P 值

回归                 3      56.670     18.8900  56.67  0.000

  清洁小时           1       4.744      4.7444   4.74  0.029

  温度               1      38.800     38.8000  38.80  0.000

  螺丝钉的大小       1      13.126     13.1256  13.13  0.000

误差                32      31.607      0.9877

合计                35      88.277

 

 

模型汇总

 

           偏差 R-Sq

偏差 R-Sq     (调整)     AIC

   64.20%     60.80%  253.29

 

 

系数

 

                                     方差膨

项                 系数  系数标准误  胀因子

常量             4.3982      0.0628

清洁小时        0.01798     0.00826    1.00

温度          -0.001974    0.000318    1.00

螺丝钉的大小

  小            -0.1546      0.0427    1.00

 

 

回归方程

 

褪色缺陷  =  exp(Y')

 

 

螺丝钉

的大小

大      Y' = 4.398 + 0.01798 清洁小时 - 0.001974 温度

 

小      Y' = 4.244 + 0.01798 清洁小时 - 0.001974 温度

 

 

拟合优度检验

 

检验     自由度      估计     均值   卡方   P 值

偏差         32  31.60722  0.98773  31.61  0.486

Pearson      32  31.26713  0.97710  31.27  0.503

 

 

异常观测值的拟合和诊断

 

观测值  褪色缺陷  拟合值   残差  标准残差

    33     43.00   58.18  -2.09     -2.18  R

 

R  残差大

解释结果

会话窗口输出

·    偏差分析表 (0.000) 中回归模型的 p 值显示，回归过程估计的模型在 0.05 a 水平时是显著的。这表明至少有一个系数不为零。

·    偏差 R2 值表明这些预测变量可以解释褪色数中 64.20% 的方差。调整偏差 R2  为 60.80%，这说明了模型中预测变量的个数。使用这些值将此模型与其他模型比较。

·    Akaike 信息准则 (AIC) 值为 253.29。使用 AIC 比较不同的模型。AIC 性越小则越好。

·    清洁小时的系数为 0.01798。由于模型使用自然对数链接函数且系数较小，该系数表明，褪色数每小时增加约 1.8%。有关详细信息，请阅读解释参数估计。

·    一个观测值的标准化残差小于 -2，此点与模型的拟合不好。由于残差显示该模型不适用，因而无法评估点是否异常。

图形窗口输出

·    正态概率图显示一个与正态分布一致的近似线性模式。要调查单个的点，请用笔刷刷图形。

·    残差与拟合值图显示一条可区分的曲线。此模式表明该模型不适用。对于这些数据，此模式是因为螺丝钉尺寸和温度交互所致，但交互作用项不在模型内。这些结果是不可靠的，除非您添加交互作用项并得到令人满意的残差图。

·    在直方图中没有残差看起来异常。区间中有三个残差，包括 -2 和 2。您可以检查其中一个残差在其他残差图上是否小于 -2。

·    残差与顺序图以 9 个负残差开头。残差的中间部分往往比开头位置和数据集末尾位置的残差高。对于这些数据，此模式还是因为缺少交互作用的缘故。由于数据不是按随机顺序收集的，因此缺少的交互作用看起来像时间效应。

有关残差图的详细信息，请参阅检查模型和识别异常值。